题目内容
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。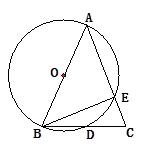
(1)求∠EBC的度数;
(2)求证:BD=CD。
【答案】
(1)解:∵AB为⊙O的直径,
∴∠AEB=∠CEB=90°,
又∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BAC=45°,
∴∠ABC=∠ACB=67.5°,
∴∠EBC=90°-67.5°=22.5°,
(2)证明:连接AD,
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
即AD⊥BC,
又∵AB=AC,
∴BD=CD,
【解析】(1)由圆周角定理得出∠AEB=∠CEB=90°,又由等腰三角形的性质得出∠ABC=∠ACB,再根据三角形内角和得出∠ABC=∠ACB=67.5°,
∠EBC=22.5°.
(2)连接AD,由圆周角定理得出∠AEB=∠CEB=90°,即AD⊥BC;又由等腰三角形的性质得出BD=CD.
【考点精析】关于本题考查的三角形的内角和外角和等腰三角形的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目