题目内容
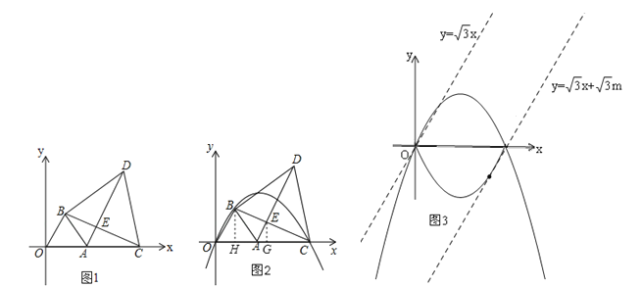
【题目】如图1,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A右侧,连接BC,以BC为边在第一象限内作等边△BCD,连接AD交BC于E.
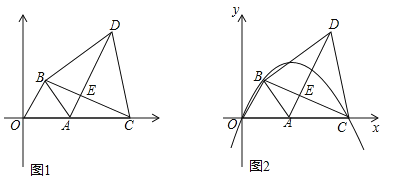
(1)①直接回答:△OBC与△ABD全等吗?
②试说明:无论点C如何移动,AD始终与OB平行;
(2)当点C运动到使AC2=AEAD时,如图2,经过O、B、C三点的抛物线为y1.试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的条件下,将y1沿x轴翻折得y2,设y1与y2组成的图形为M,函数![]() 的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
【答案】(1)①△OBC与△ABD全等;②证明见解析;(2)P(3,![]() )或(﹣2,
)或(﹣2,![]() );(3)﹣
);(3)﹣![]() ≤m<0.
≤m<0.
【解析】
试题分析:(1)①利用等边三角形的性质证明△OBC≌△ABD;
②证明∠OBA=∠BAD=60°,可得OB∥AD;
(2)首先证明DE⊥BC,再求直线AE与抛物线的交点就是点P,所以分别求直线AE和抛物线y1的解析式组成方程组,求解即可;
(3)先画出如图3,根据图形画出直线与图形M有个公共点时,两个边界的直线,上方到![]() ,将
,将![]() 向下平移即可满足l与图形M有3个公共点,一直到直线l与y2相切为止,主要计算相切时,列方程组,确定△≥0时,m的值即可.
向下平移即可满足l与图形M有3个公共点,一直到直线l与y2相切为止,主要计算相切时,列方程组,确定△≥0时,m的值即可.
试题解析:(1)①△OBC与△ABD全等,理由是:如图1,∵△OAB和△BCD是等边三角形,∴∠OBA=∠CBD=60°,OB=AB,BC=BD,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,∴△OBC≌△ABD(SAS);
②∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,∴∠OBA=∠BAD,∴OB∥AD,∴无论点C如何移动,AD始终与OB平行;
(2)如图2,∵AC2=AEAD,∴![]() ,∵∠EAC=∠DAC,∴△AEC∽△ACD,∴∠ECA=∠ADC,∵∠BAD=∠BAO=60°,∴∠DAC=60°,∵∠BED=∠AEC,∴∠ACB=∠ADB,∴∠ADB=∠ADC,∵BD=CD,∴DE⊥BC,Rt△ABE中,∠BAE=60°,∴∠ABE=30°,∴AE=
,∵∠EAC=∠DAC,∴△AEC∽△ACD,∴∠ECA=∠ADC,∵∠BAD=∠BAO=60°,∴∠DAC=60°,∵∠BED=∠AEC,∴∠ACB=∠ADB,∴∠ADB=∠ADC,∵BD=CD,∴DE⊥BC,Rt△ABE中,∠BAE=60°,∴∠ABE=30°,∴AE=![]() AB=
AB=![]() ×2=1,Rt△AEC中,∠EAC=60°,∴∠ECA=30°,∴AC=2AE=2,∴C(4,0),等边△OAB中,过B作BH⊥x轴于H,∴BH=
×2=1,Rt△AEC中,∠EAC=60°,∴∠ECA=30°,∴AC=2AE=2,∴C(4,0),等边△OAB中,过B作BH⊥x轴于H,∴BH=![]() =
=![]() ,∴B(1,
,∴B(1,![]() ),设y1的解析式为:y=ax(x﹣4),把B(1,
),设y1的解析式为:y=ax(x﹣4),把B(1,![]() )代入得:
)代入得:![]() =a(1﹣4),a=﹣
=a(1﹣4),a=﹣![]() ,∴设y1的解析式为:y1=﹣
,∴设y1的解析式为:y1=﹣![]() x(x﹣4)=
x(x﹣4)=![]() ,过E作EG⊥x轴于G,Rt△AGE中,AE=1,∴AG=
,过E作EG⊥x轴于G,Rt△AGE中,AE=1,∴AG=![]() AE=
AE=,EG=
![]() =
=![]() ,∴E(
,∴E(![]() ,
,![]() ),设直线AE的解析式为:y=kx+b,把A(2,0)和E(
),设直线AE的解析式为:y=kx+b,把A(2,0)和E(![]() ,
,![]() )代入得:
)代入得: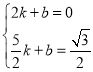 ,解得:
,解得: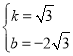 ,∴直线AE的解析式为:
,∴直线AE的解析式为:![]() ,则
,则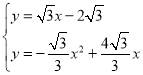 ,解得:
,解得: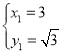 ,
,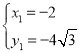 ,∴P(3,
,∴P(3,![]() )或(﹣2,
)或(﹣2,![]() );
);
(3)如图3,y1=![]() =
=![]() ,顶点(2,
,顶点(2,![]() ),∴抛物线y2的顶点为(2,﹣
),∴抛物线y2的顶点为(2,﹣![]() ),∴y2=
),∴y2=![]() ,当m=0时,
,当m=0时,![]() 与图形M两公共点,当y2与l相切时,即有一个公共点,l与图形M有3个公共点,则:
与图形M两公共点,当y2与l相切时,即有一个公共点,l与图形M有3个公共点,则: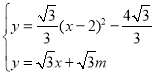 ,
,![]() ,x2﹣7x﹣3m=0,△=(﹣7)2﹣4×1×(﹣3m)≥0,m≥﹣
,x2﹣7x﹣3m=0,△=(﹣7)2﹣4×1×(﹣3m)≥0,m≥﹣![]() ,∴当l与M的公共点为3个时,m的取值是:﹣
,∴当l与M的公共点为3个时,m的取值是:﹣![]() ≤m<0.
≤m<0.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案