题目内容
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() .
.

(1)求该抛物线和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的动点,设
上方抛物线上的动点,设![]() 点的横坐标为
点的横坐标为![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积,并求出
的面积,并求出![]() 面积的最大值;
面积的最大值;
(3)设P点是直线![]() 上一动点,
上一动点,![]() 为抛物线上的点,是否存在点
为抛物线上的点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、P、
、P、![]() 为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点
为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点![]() 坐标,不存在说明理由.
坐标,不存在说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 有最大值为4;(3)存在,
有最大值为4;(3)存在,![]() 坐标
坐标![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据抛物线的对称性求得点B坐标,然后利用待定系数法分别求函数解析式即可;
(2)设![]() 点坐标
点坐标![]() ,过
,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() 点,则
点,则![]() 坐标为
坐标为![]() ,然后根据三角形面积公式求得
,然后根据三角形面积公式求得![]() ,从而用二次函数的性质求得其最值;
,从而用二次函数的性质求得其最值;
(3)利用平行四边形的性质,分四边形CPMB是平行四边形时,BN=PK=1;四边形CMPB是平行四边形时,CN=BO-1=3;四边形CPBM是平行四边形时,BN=OP=1三种情况确定M点横坐标,从而代入二次函数解析式求M点坐标.
解:(1)∵![]() ,对称轴为直线
,对称轴为直线![]() .
.
∴![]()
设二次函数解析式为![]()
将C(0,2)代入解析式,得![]() ,解得
,解得![]()
∴![]()
∴抛物线解析式为:![]() ,
,
设直线BC的解析式为![]()
将B(4,0)、C(0,2)代入解析式,得
![]() ,解得
,解得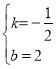
∴直线![]() 解析式为
解析式为![]()
(2)过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于
于![]() 点,
点,
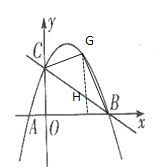
设![]() 点坐标
点坐标![]() ,则
,则![]() 坐标为
坐标为![]()
∴![]()
∴![]()
∵a=-1<0
∴当![]() 时,
时,![]() 有最大值为4.
有最大值为4.
(3)存在
设M点坐标为![]()
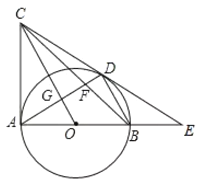
如图,过点M作MN⊥x轴,过点P作PK⊥y轴,
①当四边形CPMB是平行四边形时,BN=PK=1
∴a=5
∴![]()
∴此时M点坐标为(5,-3)
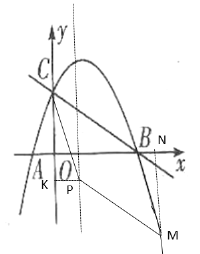
②当四边形CMPB是平行四边形时,CN=BO-1=3
∴a=-3
∴![]()
∴此时M点坐标为(-3,-7)
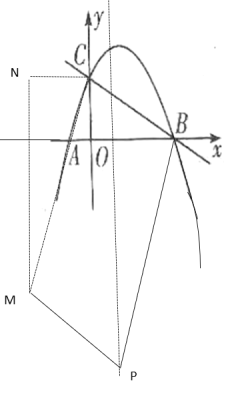
③当四边形CPBM是平行四边形时,BN=OP=1
∴a=3
∴![]()
∴此时M点坐标为(3,2)

综上所述,![]() 坐标为
坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目