题目内容
【题目】(教材呈现)下图是华师版九年级上册数学教材第103—104页的部分内容.

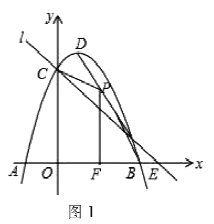
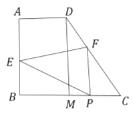
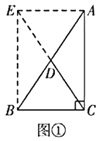
定理证明:请根据教材图24.2.2的提示,结合图①完成直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”的证明.
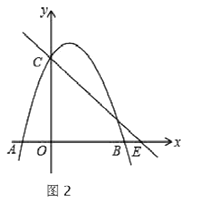
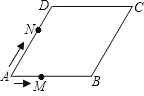
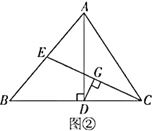
定理应用:如图②,在![]() 中,
中,![]() ,垂足为点
,垂足为点![]() (点
(点![]() 在
在![]() 上),
上),![]() 是
是![]() 边上的中线,
边上的中线,![]() 垂直平分
垂直平分![]() .求证:
.求证:![]() .
.
【答案】定理证明:见详解;定理应用:见详解.
【解析】
定理证明:延长CD到点E,使CD=DE,通过条件证明四边形EBCA为矩形,利用矩形的性质可得到结论;
定理应用:连接ED,通过定理得到DE=BE,即∠B=∠EDB,然后通过![]() 垂直平分
垂直平分![]() ,得到DE=DC,即∠DEC=∠BCE,利用三角形外角可证得结论.
,得到DE=DC,即∠DEC=∠BCE,利用三角形外角可证得结论.
定理证明:延长CD到点E,使CD=DE,连接AE、BE,
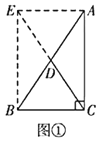
∵DC是AB边上的中线,
∴AD=BD,
又∵CD=DE,
∴四边形EBCA为平行四边形,
又∵∠ACB为直角,
∴四边形EBCA为矩形,
∴AB=CE,
∴![]() ,
,
∴直角三角形斜边上的中线等于斜边的一半;
定理应用:连接ED,
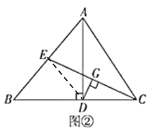
∵△ABC中,![]() 是
是![]() 边上的中线,
边上的中线,
∴E为AB的中点,
又∵![]() ,
,
∴DE是直角三角形ABD斜边上的中线,
∴DE=BE,
∴∠B=∠EDB,
∵![]() 垂直平分
垂直平分![]() ,
,
∴DE=DC,
∴∠DEC=∠BCE,
∵∠EDB=∠DEC+∠BCE,
∴∠EDB=2∠BCE,
∴![]() .
.

练习册系列答案
相关题目
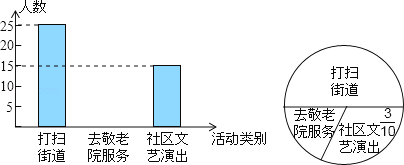
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.