题目内容
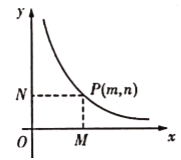
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
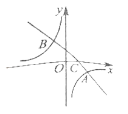
(1)请直接写出不等式![]() 的解集;
的解集;
(2)将![]() 轴下方的图象沿
轴下方的图象沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 的面积为8.
的面积为8.
【解析】
(1)根据函数图像,一次函数和反比例函数的交点坐标确定不等式![]() 的解集;
的解集;
(2)将A点坐标代入反比例函数解析式求![]() ,确定反比例函数解析式,然后利用反比例函数解析式求点B坐标,然后将A,B坐标代入一次函数解析式,待定系数法求函数解析式;从而确定C点坐标,然后根据翻着的性质求得
,确定反比例函数解析式,然后利用反比例函数解析式求点B坐标,然后将A,B坐标代入一次函数解析式,待定系数法求函数解析式;从而确定C点坐标,然后根据翻着的性质求得![]() ,从而求三角形面积.
,从而求三角形面积.
解:(1)根据函数图象可知![]() 或
或![]() .
.
(2)将![]() 代入
代入![]() 得
得![]() ,
,
∴![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() ,
,
将![]() ,
,![]() 代入
代入![]()
得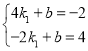
解得![]() ,
,
∴一次函数的关系式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴图象沿![]() 轴翻折后得
轴翻折后得![]() ,
,
![]() ,
,
∴![]() 的面积为8.
的面积为8.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目