Question

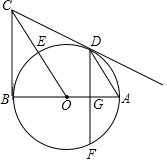
【题目】如图，△ABC内接于⊙O，AB＝AC，∠BAC＜60°，AD为的直径，BE⊥AC交AD于P，BE的延长线交⊙O于点F，连结AF，CF，AD交BC于G，在不添加其他辅助线的情况下，图中除AB＝AC外，相等的线段共有（　　）对．

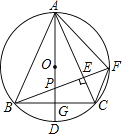
A.2B.3C.4D.5

Answer 1

【答案】C

【解析】

根据垂径定理得到BG＝CG，连接CP，根据等腰三角形的性质得到PB＝PC，根据余角的性质得到∠PAE＝∠GBP，推出∠APE＝∠AFE，得到AP＝AF，根据等腰三角形的性质即可得到结论．

解：∵AB＝AC，

∴，

∵AD经过圆心O，

∴AD⊥BC，

∴BG＝CG，

如图，连接CP，

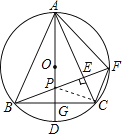
∵AB＝AC，AD⊥BC，

∴PB＝PC，

∵BF⊥AC，

∴∠AEP＝∠BGP＝90°，

∴∠PAE+∠APE＝90°，∠GBP+∠BPG＝90°，

∵∠APE＝∠BPG，

∴∠PAE＝∠GBP，

∵∠EAF＝∠GBP，

∴∠EAF＝∠EAP，

∵∠EAP+∠APE＝90°，∠EAF+∠AFE＝90°，

∴∠APE＝∠AFE，

∴AP＝AF，

∵AC⊥FP，

∴EP＝FE，

∴CP＝CF＝BP，

∴相等的线段共有4对，

故选：C．