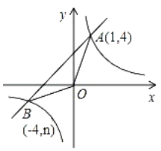
题目内容
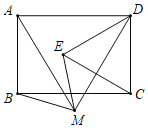
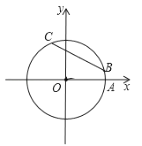
【题目】如图,四边形ABDC内接于⊙O,AB是⊙O的直径,OD⊥BC于点E.
(1)请你写出两个不相同的结论(不添加辅助线);
(2)连接AD,若BE=4,AC=6,求线段AD的长.
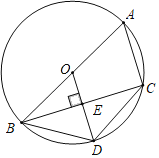
【答案】(1)∠ACB=90°,BE=CE ;(2)AD=4![]() .
.
【解析】
(1)由AB为圆的直径,利用直径所对的圆周角为直角可得出∠ACB=90°;由OD垂直于BC,利用垂径定理得到E为BC的中点,即BE=CE;
(2)由OD垂直于BC,利用垂径定理得到E为BC的中点,由BE的长求出BC的长,由AB为圆的直径,利用直径所对的圆周角为直角可得出∠ACB为直角,在直角三角形ABC中,由BC与AC的长,利用勾股定理求出AB的长,进而求出半径OB与OD的长,在直角三角形BOE中,由OB与BE的长,利用勾股定理求出OE的长,由OD﹣OE即可求出DE的长,利用勾股定理求出BD即可解决问题.
解:(1)由题意得:∠ACB=90°;BE=CE(答案不唯一);
(2)∵OD⊥BC,BE=4,
∴BE=CE=4,即BC=2BE=8,
∵AB为圆O的直径,
∴∠ACB=90°,
在Rt△ABC中,AC=6,BC=8,
根据勾股定理得:AB=![]() ,
,
∴OB=OD=5,
在Rt△OBE中,OB=5,BE=4,
根据勾股定理得:OE=![]() ,
,
则ED=OB﹣OE=5﹣3=2,BD=![]() ,
,
∵AB是直径,
∴∠ADB=90°,
∴AD=![]() .
.

练习册系列答案
相关题目