题目内容
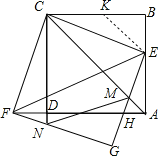
【题目】如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
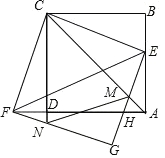
(1)证明:点A、D、F在同一条直线上;
(2)随着点E的移动,线段DH是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连结EF、MN,当MN∥EF时,求AE的长.
【答案】(1)见解析;(2)有最小值,DH的最小值为![]() ;(3)AE= 2
;(3)AE= 2![]() .
.
【解析】
(1)要证明点A、D、F在同一条直线上,只需证明∠CDF+∠CDA=180°即可.根据题中的已知条件很容易证明△DCF≌△BCE,则∠CDF=∠B=90°,结论可证.
(2)设AE=x,DH=y,通过已知条件证明△ECB∽△HEA,利用相似三角形的性质可知![]() ,即可得到一个y与x的二次函数,根据二次函数的最值可求出线段DH的最小值.
,即可得到一个y与x的二次函数,根据二次函数的最值可求出线段DH的最小值.
(3)利用矩形的性质及平行线的性质可证明△CFN≌△CEM,进而推出∠FCN=∠ECM=∠BCE=22.5°. 在BC上取一点K,使得KC=KE,则△BKE是等腰直角三角形,设BE=BK=a,则KC=KE=![]() a,利用
a,利用![]() 求出a的值,从而利用
求出a的值,从而利用![]() 即可求AE的长.
即可求AE的长.
(1)证明:∵四边形ABCD是正方形,
∴CD=CB,∠BCD=∠B=∠ADC=90°,
∵CE=CF,∠ECF=90°,
∴∠ECF=∠DCB,
∴∠DCF=∠BCE,
∴△DCF≌△BCE,
∴∠CDF=∠B=90°,
∴∠CDF+∠CDA=180°,
∴点A、D、F在同一条直线上.
(2)解:有最小值.
理由:设AE=x,DH=y,则AH=1-y,BE=1-x,
∵四边形CFGE是矩形,
∴∠CEG=90°,
∴∠CEB+∠AEH=90°
CEB+∠ECB=90°,
∴∠ECB=∠AEH,
∵∠B=∠EAH=90°,
∴△ECB∽△HEA,
![]()
即![]()
![]()
∵a=1>0,
∴当![]() 时,y有最小值,最小值为
时,y有最小值,最小值为![]() ,
,
∴DH的最小值为![]() .
.
(3)解:∵四边形CFGE是矩形,CF=CE,
∴四边形CFGE是正方形,
∴GF=GE,∠GFE=∠GEF=45°,
∵NM∥EF,
∴∠GNM=∠GFE,∠GMN=∠GEF,
∴∠GMN=∠GNM,
∴GN=GM,
∴FN=EM,
∵CF=CE,∠CFN=∠CEM,
∴△CFN≌△CEM,
∴∠FCN=∠ECM,
∵∠MCN=45°,
∴∠FCN=∠ECM=∠BCE=22.5°,
在BC上取一点K,使得KC=KE
![]()
![]()
![]()
∴△BKE是等腰直角三角形
设BE=BK=a,则KC=KE=![]() a,
a,
![]()
![]()
![]()

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案