题目内容
【题目】如图,在![]() 中,
中,![]() 点
点![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 与点
与点![]() 不重合),过动点
不重合),过动点![]() 作
作![]() 交
交![]() 于点
于点![]()
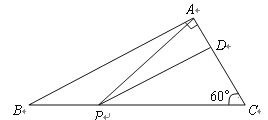
(1)若![]() 与
与![]() 相似,则
相似,则![]() 是多少度?
是多少度?
(2)试问:当![]() 等于多少时,
等于多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)若以线段![]() 为直径的圆和以线段
为直径的圆和以线段![]() 为直径的圆相外切,求线段
为直径的圆相外切,求线段![]() 的长.
的长.
【答案】(1)60°或30°.(2)PC等于12时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .(3)
.(3)![]()
【解析】
(1)当△ABC与△DAP相似时,应有∠APD=∠B或∠APD=∠C,即∠APD为30°或60°.
(2)设PC=x,由PD∥BA,得∠BAC=∠PDC=90°,∴AC=BCcos60°=12,CD=xcos60°=![]() x,AD=12-
x,AD=12-![]() x,而PD=xsin60°=
x,而PD=xsin60°=![]() x,∴S△APD=
x,∴S△APD=![]() PDAD把PD,AD的值代入,得到S△APD=
PDAD把PD,AD的值代入,得到S△APD=![]() .∴PC等于12时,△APD的面积最大,最大面积是18
.∴PC等于12时,△APD的面积最大,最大面积是18![]() .
.
(3)设以BP和AC为直径的圆心分别为O1、O2,过O2作O2E⊥BC于点E,设⊙O1的半径为x,则BP=2x,AC=12,∴O2C=6,∴CE=6cos60°=3.∴由勾股定理得,O2E=![]() ,O1E=21-x,由于⊙O1和⊙O2外切,则圆心距O1O2=x+6.在Rt△O1O2E中,有O1O22=O2E2+O1E2,即(x+6)2=(21-x)2+(3
,O1E=21-x,由于⊙O1和⊙O2外切,则圆心距O1O2=x+6.在Rt△O1O2E中,有O1O22=O2E2+O1E2,即(x+6)2=(21-x)2+(3![]() )2,求解得到x的值,进而求得BP的值.
)2,求解得到x的值,进而求得BP的值.
(1)当△ABC与△DAP相似时,∠APD的度数是60°或30°.
(2)设![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,而
,而![]() ,
,
∴![]()
![]() .
.
∴PC等于12时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .
.
(3)设以![]() 和
和![]() 为直径的圆心分别为
为直径的圆心分别为![]() 、
、![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
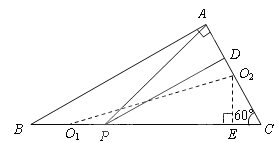
设![]() 的半径为
的半径为![]() ,则
,则![]() .显然,
.显然,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 外切,∴
外切,∴![]() .
.
在![]() 中,有
中,有![]() ,
,
∴![]() ,解得:
,解得:![]() , ∴
, ∴![]()

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】某网上书店以每本24元的价格购进了600本某种畅销书籍(定价每本45元),第一个月以每本36元销售,卖出了200本;第二个月书店为了增加销售量,决定在第一个月价格的基础上降价销售,根据市场调查,每本书每降低1元,可多售出20本,但最低售价应高于购进的价格.第二个月结束后,书店将剩余的书籍捐赠给某希望学校,设第二个月每本降低![]() 元.
元.

(1)填表:(列式,不需要化简)
时间 | 第一个月 | 第二个月 |
每本售价(元) | 36 | |
销售量(本) | 200 |
(2)如果该书店希望通过销售这批书籍获利2400元,那么第二个月每本书的售价应是多少元?