题目内容
【题目】杰瑞公司成立之初投资1500万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元.按规定,该产品售价不得低于100元/件且不得超过180元/件,该产品销售量y(万件)与产品售价x(元)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或者亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1340万元,若能,求出第二年产品售价;若不能,请说明理由.
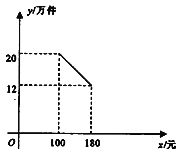
【答案】(1)100≤x≤180 (2) 定为180元/件时,最小亏损为60万元 (3)见解析
【解析】(1)设y=kx+b,则由图象可求得k,b,从而得出y与x之间的函数关系式,并写出x的取值范围100≤x≤180;
(2)设公司第一年获利W万元,则可表示出W=-![]() (x-180)2-60≤-60,则第一年公司亏损了,当产品售价定为180元/件时,亏损最小,最小亏损为60万元;
(x-180)2-60≤-60,则第一年公司亏损了,当产品售价定为180元/件时,亏损最小,最小亏损为60万元;
(3)假设两年共盈利1340万元,则-![]() x2+36x-1800-60=1340,解得x的值,根据100≤x≤180,则x=160时,公司两年共盈利达1340万元.
x2+36x-1800-60=1340,解得x的值,根据100≤x≤180,则x=160时,公司两年共盈利达1340万元.
(1)设y=kx+b,则由图象知:![]() ,
,
解得k=-![]() ,b=30,
,b=30,
∴y=-![]() x+30,100≤x≤180;
x+30,100≤x≤180;
(2)设公司第一年获利W万元,
则W=(x-60)y-1500=-![]() x2+36x-3300=-
x2+36x-3300=-![]() (x-180)2-60≤-60,
(x-180)2-60≤-60,
∴第一年公司亏损了,当产品售价定为180元/件时,亏损最小,最小亏损为60万元;
(3)若两年共盈利1340万元,
因为第一年亏损60万元,第二年盈利的为(x-60)y=-![]() x2+36x-1800,
x2+36x-1800,
则-![]() x2+36x-1800-60=1340,
x2+36x-1800-60=1340,
解得x1=200,x2=160,
∵100≤x≤180,∴x=160,
∴每件产品的定价定为160元时,公司两年共盈利达1340万元.

【题目】某铁路桥长1000米.现有一列火车从桥上匀速通过.测得火车从开始上桥到完全通过桥共用了1分钟(即从车头进入桥头到车尾离开桥尾),整个火车完全在桥上的时间为40秒.
(1)如果设这列火车的长度为x米,填写下表(不需要化简):
火车行驶过程 | 时间(秒) | 路程(米) | 速度(米/秒) |
完全通过桥 | 60 | ||
整列车在桥上 | 40 |
(2)求这列火车的长度.
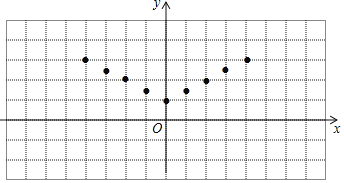
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .