ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈΣ Β ©ΓΑ≈©¥εΝτ ΊΕυΆ·ΙΊΑ°ΦΤΜ°Γ±Θ§Ρ≥–ΘΫα»Ϊ–ΘΗςΑύΝτ ΊΕυΆ·ΒΡ»Υ ΐ«ιΩωΫχ––ΝΥΆ≥ΦΤΘ§ΖΔœ÷ΗςΑύΝτ ΊΕυΆ·»Υ ΐ÷Μ”–1ΟϊΓΔ2ΟϊΓΔ3ΟϊΓΔ4ΟϊΓΔ5ΟϊΓΔ6ΟϊΙ≤Νυ÷÷«ιΩωΘ§≤Δ÷Τ≥…»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ
Θ®1Θ©«σΗΟ–ΘΤΫΨυΟΩΑύ”–Εύ…ΌΟϊΝτ ΊΕυΆ·ΘΩ≤ΔΫΪΗΟΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®2Θ©Ρ≥Α°–Ρ»Υ ΩΨωΕ®¥”÷Μ”–2ΟϊΝτ ΊΕυΆ·ΒΡ’β–©ΑύΦΕ÷–Θ§»Έ―ΓΝΫΟϊΫχ––…ζΜνΉ ÷ζΘ§«κ”ΟΝ–±μΖ®ΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®Θ§«σ≥ωΥυ―ΓΝΫΟϊΝτ ΊΕυΆ·ά¥Ή‘Ά§“ΜΗωΑύΦΕΒΡΗ≈¬ Θ°
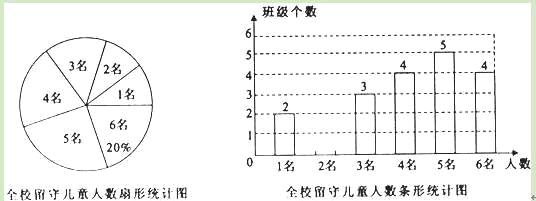
ΓΨ¥πΑΗΓΩΫβΘΚΘ®1Θ©ΗΟ–ΘΑύΦΕΗω ΐΈΣ4Γ¬20%=20Θ®ΗωΘ©Θ§
÷Μ”–2ΟϊΝτ ΊΕυΆ·ΒΡΑύΦΕΗω ΐΈΣΘΚ20©¹Θ®2+3+4+5+4Θ©=2Θ®ΗωΘ©Θ§
ΗΟ–ΘΤΫΨυΟΩΑύΝτ ΊΕυΆ·ΒΡ»Υ ΐΈΣΘΚ
![]() =4Θ®ΟϊΘ©Θ§
=4Θ®ΟϊΘ©Θ§
≤ΙΆΦ»γœ¬ΘΚ

Θ®2Θ©”…Θ®1Θ©ΒΟ÷Μ”–2ΟϊΝτ ΊΕυΆ·ΒΡΑύΦΕ”–2ΗωΘ§Ι≤4Οϊ―ß…ζΘ°…ηA1Θ§A2ά¥Ή‘“ΜΗωΑύΘ§B1Θ§B2ά¥Ή‘“ΜΗωΑύΘ§

”– ςΉ¥ΆΦΩ…÷ΣΘ§Ι≤”–12÷–Β»Ω…ΡήΒΡ«ιΩωΘ§Τδ÷–ά¥Ή‘“ΜΗωΑύΒΡΙ≤”–4÷÷«ιΩωΘ§
‘ρΥυ―ΓΝΫΟϊΝτ ΊΕυΆ·ά¥Ή‘Ά§“ΜΗωΑύΦΕΒΡΗ≈¬ ΈΣΘΚ![]() =
=![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
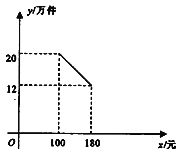
Θ®1Θ© Ήœ»«σ≥ωΑύΦΕ ΐΘ§»ΜΚσΗυΨίΧθ–ΈΆ≥ΦΤΆΦ«σ≥ω÷Μ”–2ΟϊΝτ ΊΕυΆ·ΒΡΑύΦΕ ΐΘ§‘Ό«σ≥ωΉήΒΡΝτ ΊΕυΆ· ΐΘ§ΉνΚσ«σ≥ωΟΩΑύΤΫΨυΝτ ΊΕυΆ· ΐΘΜ
Θ®2Θ©άϊ”Ο ςΉ¥ΆΦ»ΖΕ®Ω…Ρή÷÷ ΐΚΆά¥Ή‘Ά§“ΜΑύΒΡ÷÷ ΐΘ§»ΜΚσΨΆΡήΥψ≥ωά¥Ή‘Ά§“ΜΗωΑύΦΕΒΡΗ≈¬ .

 –¬ΥΦΈ§ΦΌΤΎΉς“Β νΦΌΦΣΝ÷¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
–¬ΥΦΈ§ΦΌΤΎΉς“Β νΦΌΦΣΝ÷¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ άΕΧλΫΧ”ΐ νΦΌ”≈Μ·―ßœΑœΒΝ–¥πΑΗ
άΕΧλΫΧ”ΐ νΦΌ”≈Μ·―ßœΑœΒΝ–¥πΑΗ