题目内容
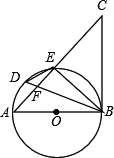
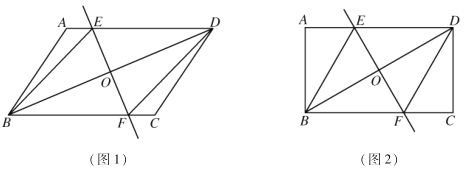
【题目】已知:在![]() 中,作对角线
中,作对角线![]() 的垂直平分线
的垂直平分线![]() ,垂足为点
,垂足为点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,当![]() ,且
,且![]() 时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于
时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于![]() 长度的
长度的![]() 倍.
倍.
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)证明![]() ,得到OE=OF,再结合OB=OD得出结论;
,得到OE=OF,再结合OB=OD得出结论;
(2)证明Rt△ABE≌Rt△OBE,AB=OB,∠ABE=∠OBE=∠OBF,从而推出∠OBE=30°,再根据直角三角形的性质以及矩形和菱形的性质得到OB=![]() OE=OD=AB=CD即可.
OE=OD=AB=CD即可.
解:(1)证明:如图1,∵四边形![]() 是平行四边形,
是平行四边形,
∴![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中,
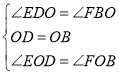 ,
,
∴![]() (ASA),
(ASA),
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴![]() 为菱形;
为菱形;
(2)如图2,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵AE=OF,四边形BFDE为菱形,
∴OE=OF=AE,∠EOB=90°,
在Rt△ABE和Rt△OBE中,
![]() ,
,
∴Rt△ABE≌Rt△OBE(HL),
∴AB=OB,∠ABE=∠OBE=∠OBF,
∵∠ABC=90°,
∴∠OBE=30°,
∴2OE=BE,
∴OB=![]() OE=OD=AB=CD,
OE=OD=AB=CD,
故答案为:OB,OD,AB,CD.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目