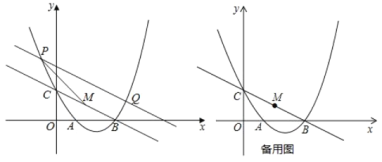
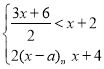题目内容
【题目】如图,把一个等腰直角三角形放在平面直角坐标系中,∠ACB=90°,点C(-1,0),点B在反比例函数![]() 的图像上,且y轴平分∠BAC,则k的值是_________.
的图像上,且y轴平分∠BAC,则k的值是_________.

【答案】![]()
【解析】
作BE⊥x轴,垂直为E,先证明△AOC≌△CEB,得OC=BE=1,AO=CE;再证明△AOC≌△AOD,得OC=OD=1;设DE=m,通过证明△BED∽△AOD,构造方程,求出m,确定E的坐标,即可求解.
解:作BE⊥x轴,垂直为E,则∠BEC=90°,
∴∠CBE+∠BCE=90°,
∵△ABC为等腰直角三角形,
∴AC=CB,∠ACB=90°,
∴∠ACO+∠BCE=90°,
∴∠ACO=∠CBE,
∵∠AOC=∠CEB=90°,
∴△AOC≌△CEB,
∴OC=BE=1,AO=CE.
∵y轴平分∠BAC,
∴∠CAO=∠DAO,
∵OA=OA, ∠AOC=∠AOD=90°,
∴△AOC≌△AOD,
∴OC=OD=1.
设DE=m,则CE=OA=2+m,
∵BE∥OA,
∴△BED∽△AOD,
∴![]() ,
,
即: ![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴OE=OD+DE=![]() ,
,
∴点B的坐标为(![]() ),
),
∴![]() .
.

故答案为:![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()