��Ŀ����
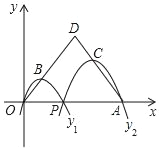
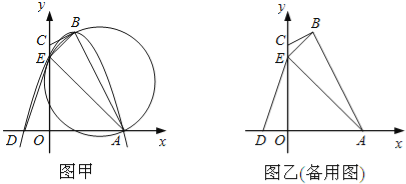
����Ŀ����ͼ��������y��ax2+x+c��x�ύ��A��B���㣬A������Ϊ����3��0������y�ύ�ڵ�C����C����Ϊ��0����6��������BC����C����x��ĶԳƵ�D����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1������κ�������ʽ��
��2����P��x�����˶�������6��m��2ʱ�����߶�MQ���ȵ����ֵ��
��3����P��x�����˶�ʱ��NΪƽ����һ�㣬ʹ�õ�B��C��M��NΪ������ı���Ϊ���Σ�������ڣ���ֱ��д����N���ꣻ�����ڣ�˵�����ɣ�

���𰸡���1��y��x2+x��6����2��MQ�����ֵΪ16����3��N����Ϊ����![]() ����
����![]() ����2��0����7.2��3.6����2����12�������ɼ�����.
����2��0����7.2��3.6����2����12�������ɼ�����.
��������
��1����A������Ϊ��-3��0������C����Ϊ��0��-6��������κ�������ʽ����ã�a=1��c=-6���ʣ����κ�������ʽΪy=x2+x-6��
��2����C����x��ĶԳƵ�D��0��6����MQ=yM-yQ=-3m+6-��m2+m-6��=-��m+2��2+16��������⣻
��3���ٵ�BC��Ϊ���εı�ʱ��N��Ӧ����x�ᣬ����B��Գƣ�����N����Ϊ��-2��0�����ڵ�BC��Ϊ���εĶԽ���ʱ����BC�Ĵ�ֱƽ����MH��ֱ��BD��ֱ��MH���㼴ΪM����Ϊ��������⣮
��1����A������Ϊ����3��0������C����Ϊ��0����6��������κ�������ʽ��
��ã�a��1��c����6��
�ʣ����κ�������ʽΪy��x2+x��6��
��2����C����x��ĶԳƵ�D��0��6����
��B��D�������ڵ�ֱ�߷���Ϊ��y����3x+6��
��M������m����3m+6������Q��m��m2+m��6����
��MQ��yM��yQ����3m+6����m2+m��6��������m+2��2+16��
�ک�6��m��2ʱ���������㴦��ȡ�����ֵ��
��MQ�����ֵΪ16��
��3���ٵ�BC��Ϊ���εı�ʱ��
���һ��N��Ӧ����x�ᣬ����B��Գƣ�����N����Ϊ����2��0����
�������BC��MB�����������ڱߣ���BC��BM�����N����Ϊ��2����12����
�������BC��CMΪ�ڱ�ʱ�����N����Ϊ��7.2��3.6����
�ڵ�BC��Ϊ���εĶԽ���ʱ����BC�Ĵ�ֱƽ����MH��
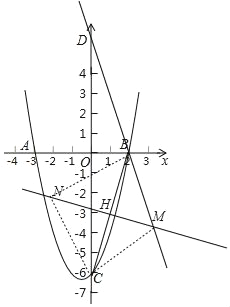
��ֱ��DB��MH�Ľ���ΪM��M����BC�ĶԳƵ�ΪN��HΪBC���е㣬
��H������1����3����
ֱ��BD�ķ���Ϊ��y����3x+6��ֱ��MH�ķ���Ϊ��y=-![]() x-
x-![]() ��
��
���������������̣���ã�M����Ϊ��![]() ����
����![]() ����
����
ͬ����N����Ϊ����![]() ����
����![]() ����
����
�ʣ�N����Ϊ����![]() ����
����![]() ����2��0����7.2��3.6����2����12����
����2��0����7.2��3.6����2����12����