题目内容
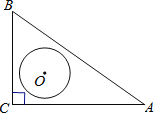
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1 B.1≤r≤![]() C.1≤r≤
C.1≤r≤![]() D.1≤r≤4
D.1≤r≤4
【答案】C
【解析】
试题分析:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,根据题意得出四边形OECF是正方形,得出OF=CF,由勾股定理得出AB=![]() =5,由内心的性质得出CF=OF=1,AF=AC﹣CF=3,由勾股定理求出OA,由直线与圆的位置关系,即可得出结果.
=5,由内心的性质得出CF=OF=1,AF=AC﹣CF=3,由勾股定理求出OA,由直线与圆的位置关系,即可得出结果.
解:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连接OA、OB,如图所示

则四边形OECF是正方形,
∴OF=CF=OE=CE,
∵∠C=90°,AC=4,BC=3,
∴AB=![]() =5,
=5,
∵O是△ABC的内心,
∴CE=CF=OF=OE=![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∴AF=AC﹣CF=3,BE=BC﹣CE=2,
∴OA=![]() =
=![]() =
=![]() ,OB=
,OB=![]() =
=![]() =
=![]() ,
,
当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当1<r≤![]() 时,以O为圆心,r为半径的圆与线段AB有两个交点;
时,以O为圆心,r为半径的圆与线段AB有两个交点;
当![]() <r≤
<r≤![]() 时,以O为圆心,r为半径的圆与线段AB有1个交点;
时,以O为圆心,r为半径的圆与线段AB有1个交点;
∴以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是1≤r≤![]() ;
;
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目