Question

【题目】问题：探究函数y=|x|-1的性质．

小凡同学根据学习函数的经验，对函数y=|x|-1的图象与性质进行了探究．下面是小凡的探究过程，请补充完整：

（1）在函数y=|x|-1中，自变量x的取值范围是______________；

（2）下表是y与x的几组对应值．

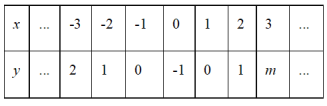
①m=_________；

②若A（n，9），B（10，9）为该函数图象上不同的两点，则n=__________；

（3）如下图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；

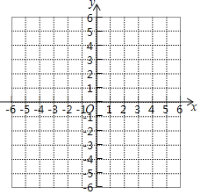
（4）结合函数图象，解决问题：

①该函数有______(填“最大值”或“最小值”)；并写出这个值为______；

②观察函数y=|x|-1的图象，写出该图象的两条性质．

Answer 1

【答案】（1）全体实数（或任意实数）；（2）①2；②-10；（3）画图见解析；（4）①当时，函数有最小值，最小值为-1；②时，y随x的增大而减小，x>0时y随x的增大而增大．函数图象为轴对称图形，对称轴为y轴等

【解析】

（1）根据题目中的函数解析式，可知x的取值范围；

（2）①根据函数解析式可以得到m的值；②根据函数解析式可以求得n的值，再根据题意得出符合题意的值；

（3）根据表格中的数据可以画出相应的函数图象；
（4）①根据函数图象即可得出函数的最小值，进而求出最小值；②根据函数图象可以写出该函数的两个性质，本题答案不唯一．

（1）由题意得：x取全体实数．

故答案是：全体实数；

（2）①当x=3时，y=|3|-1=2．

故答案是：2；

②∵ A（n，9），B（10，9）为该函数图象上不同的两点，

∴9= |x |-1,

∴x=±10,

∵B（10，9）

∴n=-10．

故答案是：-10；

（3）如图所示，即为所求；

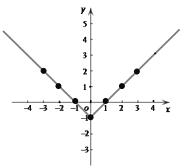
（4）①如图所示，当x=0时，函数有最小值，最小值为-1．

故答案是：最小值，-1；

②时，y随x的增大而减小，x>0时y随x的增大而增大；函数图象为轴对称图形，对称轴为y轴．