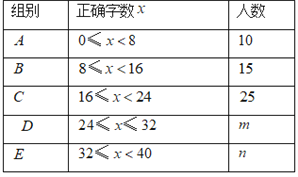
题目内容

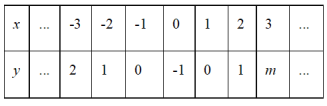
【题目】如图，由四个全等的直角三角形拼成的大正方形的面积为84，中间小正方形的面积为24，若直角三角形较长直角边为，较短直角边为，则__．

【答案】12

【解析】

根据正方形的面积公式以及勾股定理，结合图形进行分析发现：大正方形的面积即直角三角形斜边的平方84，也就是两条直角边的平方和是84，四个直角三角形的面积和是大正方形的面积减去小正方形的面积即2ab＝84-24＝60．根据完全平方公式即可求解．

解：根据题意，并结合勾股定理得：
大正方形的面积：a2＋b2＝84，
四个直角三角形面积和为：S大正方形S小正方形＝84-24＝60，
∴

∴2ab＝60，
∴(a＋b)2＝a2＋b2＋2ab＝84+60＝144

∴a+b=12
故答案为：12．

练习册系列答案
相关题目

【题目】问题：探究函数y=|x|-1的性质．

小凡同学根据学习函数的经验，对函数y=|x|-1的图象与性质进行了探究．下面是小凡的探究过程，请补充完整：

（1）在函数y=|x|-1中，自变量x的取值范围是______________；

（2）下表是y与x的几组对应值．

①m=_________；

②若A（n，9），B（10，9）为该函数图象上不同的两点，则n=__________；

（3）如下图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；

（4）结合函数图象，解决问题：

①该函数有______(填“最大值”或“最小值”)；并写出这个值为______；

②观察函数y=|x|-1的图象，写出该图象的两条性质．

【题目】（1） 2(2a 2 9b) 3(3a 2 4b)

（2）(a 2 b2)(a b)( a b)

（3） ( x 2y 3 )2 (3xy)3 (x 2 y 3)2 ( x)3 2 y 3

（4）用简便方法计算：9982 9980 16

【题目】已知y﹣3与x成正比例，且x＝2时，y＝7．

（1）求出y与x之间的函数关系；

（2）画出函数的图象；

（3）结合所画出的图象直接写出当x满足什么条件时，函数的图象都在x轴的上方？

【题目】如图在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A，B分别在x，y轴上，已知OA＝3，点D为y轴上一点，其坐标为（0，1），CD＝5，点P从点A出发以每秒1个单位的速度沿线段A﹣C﹣B的方向运动，当点P与点B重合时停止运动，运动时间为t秒

（1）求B，C两点坐标；

（2）①求△OPD的面积S关于t的函数关系式；

②当点D关于OP的对称点E落在x轴上时，求点E的坐标；

（3）在（2）②情况下，直线OP上求一点F，使FE+FA最小．

【题目】阅读以下两则材料，解决后续问题：

材料一：我们可以将任意三位数记为(其中a,b,c,分别表示该数的百位数字、十位数字和个位数字，且a≠0，显然=100a+10b+c.

材料二：若一个三位数的三个数字均不为0且三个数字互不相等，则称之为原始数，比如123就是一个原始数.将原始数的三个数位数字交换顺序，可产生出5个新的原始数，比如由123可以产生出132、213、231、312、321这5个新原始数.将这6个数相加，得到的和1332称为由原始数123生成的终止数.

问题：（1）求原始数247生成的终止数；

（2）试说明所有的原始数生成的终止数都能被222整除；

（3）若一个原始数生成的终止数为，求满足条件的所有原始数.

【题目】已知关于x的一元二次方程ax2－3x－1＝0有两个不相等的实数根，且两个实数根都在－1和0之间(不包含－1和0)，求a的取值范围．

【题目】某校举行“汉字听写”比赛，每位学生听写汉字个，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分．

根据以上信息解决下列问题：

（）在统计表中，__________，__________，并补全条形统计图．

（）扇形统计图中“组”所对应的圆心角的度数是__________．

（）若该校共有名学生，如果听写正确的个数少于个定为不合格，请你估计这所学校本次比赛听写不合格的学生人数．

【题目】甲、乙两人各射击次，甲所中的环数是，，，，，，且甲所中的环数的平均数是，众数是；乙所中的环数的平均数是，方差是4.根据以上数据，对甲，乙射击成绩的正确判断是（ ）

A.甲射击成绩比乙稳定B.乙射击成绩比甲稳定

C.甲，乙射击成绩稳定性相同D.甲、乙射击成绩稳定性无法比较

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网