题目内容
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,且AD=2,AC=BC=![]() .
.
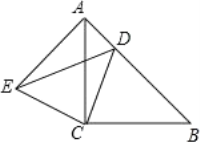
(1)证明:△ACE≌△BCD;
(2)求四边形ADCE的面积;
(3)求ED的长.
【答案】(1)见解析;(2)9;(3)![]()
【解析】
(1)根据△ACB和△ECD都是等腰直角三角形,可得:CE=CD,CA=CB,∠ECD=∠ACB=90°,再根据等式的基本性质即可得出:∠ACE=∠BCD,利用SAS即可证出△ACE≌△BCD;
(2)根据(1)中全等,四边形ADCE的面积=△ACE的面积+△ACD的面积=△BCD的面积+△ACD的面积=△ACB的面积,故计算出△ACB的面积即可;
(3)根据勾股定理即可算出AB的长,从而计算出BD的长,再根据(1)的△ACE≌△BCD即可得EA=BD,∠EAC=∠DBC=45°,从而得到∠EAD=90°,最后根据勾股定理即可算出ED的长.
解:(1)∵△ACB和△ECD都是等腰直角三角形
∴CE=CD,CA=CB,∠ECD=∠ACB=90°
∴∠ECD-∠ACD=∠ACB-∠ACD
∴∠ACE=∠BCD
在△ACE和△BCD中
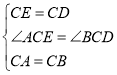
∴△ACE≌△BCD(SAS);
(2)∵△ACE≌△BCD
∴S△ACE=S△BCD
∴S四边形ADCE =S△ACE+S△ACD =S△BCD+S△ACD =S△ACB
∵AC=BC=![]()
∴S△ACB=![]()
∴S四边形ADCE =9
(3)根据勾股定理:![]()
∴BD=AB-AD=4
∵△ACE≌△BCD
∴EA=BD=4,∠EAC=∠DBC
∵△ACB是等腰直角三角形
∴∠BAC=∠DBC=45°
∴∠EAD=∠EAC+∠BAC=∠DBC+∠BAC=90°
在Rt△EAD中
根据勾股定理:![]()

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目