题目内容
【题目】某服装厂里有许多剩余的三角形边角料,找出一块△ABC,测得∠C=90°(如图),现要从这块三角形上剪出一个半圆O,做成玩具,要求:使半圆O与三角形的两边AB、AC相切,切点分别为D、C,且与BC交于点E.
(1)在图中设计出符合要求的方案示意图.(要求:尺规作图,不写作法,保留作图痕迹).
(2)Rt△ABC中,AC=3,AB=5,连接AO,求出AO的长度.

【答案】(1)作图见解析;(2)AO为![]() .
.
【解析】
(1)以∠A的平分线与BC的交点为圆心,以到C的距离为半径的半圆即为所求;
(2)连接OD,在Rt△ABC中,根据勾股定理得BC=4,根据切线的性质和线段的和差关系得到BD=2,设⊙O的半径为r,则OB=4-r,根据勾股定理求得半径,再在Rt△ACO中,根据勾股定理求得AO.
(1) 半圆O就是所求的图形,
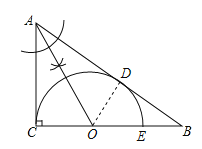
(2)连接OD,
∵Rt△ABC中,AC=3,AB=5,根据勾股定理得BC=4,
由题意可知,AB是⊙O的切线,
∴∠ODB=90°,AD=AC=3,
∴BD=2,
设⊙O的半径为r,则OB=4-r,
∴r2+22=(4-r)2.
解得![]() ,
,
在Rt△ACO中,根据勾股定理得![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目