题目内容
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2,若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
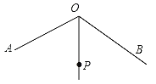
A.2个B.3个C.4个D.无数个
【答案】D
【解析】
如图在OA、OB上截取OE=OF=OP,作∠MPN=60°,只要证明△PEM≌△PON即可推出△PMN是等边三角形,由此即可得出结论.
如图在OA、OB上截取OE=OF=OP,作∠MPN=60°
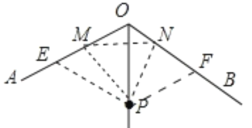
∴∠EOP=∠POF=60°,
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形,
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPO-∠OPM=∠MPN-∠OPM
∴∠EPM=∠OPN,
在△PEM和△PON中,
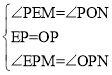
∴△PEM≌△PON(ASA).
∴PM=PN,
∵∠MPN=60°,
∴△POM是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形,
故这样的三角形有无数个.
故选D.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目