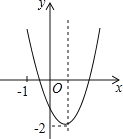题目内容
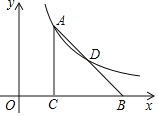
【题目】如图,某办公楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子
,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子![]() ,而当光线与地面夹角是45°时,办公楼顶
,而当光线与地面夹角是45°时,办公楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有25米的距离(
有25米的距离(![]() 在一条直线上).
在一条直线上).
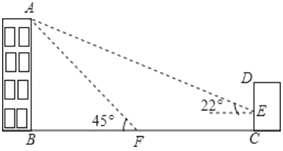
(1)求办公楼![]() 的高度;
的高度;
(2)若要在![]() ,
,![]() 之间挂一些彩旗,请你求出
之间挂一些彩旗,请你求出![]() ,
,![]() 之间的距离.(参考数据:
之间的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)教学楼的高20m;(2)A、E之间的距离约为48m.
【解析】
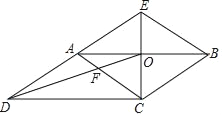
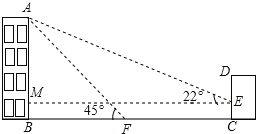
(1)如图,过点E作EM⊥AB于M,设AB为x,可得AM=x-2,ME=x+25,利用∠AEM的正切列方程求出x的值即可;
(2)利用∠AEM的余弦列方程求出AE的长即可.
如图,过点E作EM⊥AB于M,设AB为x,
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴ME=BC=BF+FC=x+25,
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,
tan22°=![]() ,
,
∴![]() ,
,
解得:x=20.
∴教学楼的高20m.
(2)由(1)可得ME=BC=x+25=20+25=45,
在Rt△AME中,cos22°=![]() ,
,
∴ ,
,
∴A、E之间的距离约为48m.

【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④
【题目】某超市销售一种商品,成本价为50元/千克,规定每千克售价不低于成本价,且不高于85元.经过市场调查,该商品每天的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系,部分数据如下表:
(元/千克)满足一次函数关系,部分数据如下表:
售价 | 50 | 60 | 70 |
销售量 | 120 | 100 | 80 |
(1)求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)设该商品每天的总利润为![]() (元),则当售价
(元),则当售价![]() 定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
(3)如果超市要获得每天不低于1600元的利润,且符合超市自己的规定,那么该商品的售价![]() 的取值范围是多少?请说明理由.
的取值范围是多少?请说明理由.