题目内容
【题目】如图，在平面直角坐标系中，在Rt△ABC中，∠ACB=90°，边BC在x轴上，点B在点C的右侧，顶点A和AB的中点D在函数
的图象上．若△ABC的面积为12，则k的值为（ ）
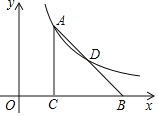
A.24B.12C.6D.6
【答案】B
【解析】
过D作DE⊥BC于E，连接AO，OD，根据相似三角形的性质得到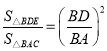
，求得S△BDE＝3，由于点A，点D在函数y＝
（k＞0，x＞0）的图象上，得到S△AOC＝S△DEO＝
，于是得到结论．
解：过D作DE⊥BC于E，连接AO，OD，
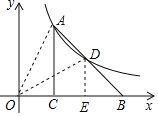
∵∠ACB=90°，∠ABC=∠DBE，
∴△BDE∽△BAC，
∴，
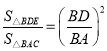∵点D是AB的中点，△ABC的面积为12，
∴S△BDE=3，
∵点A，点D在函数
的图象上，
∴
，
∵
，
∴
，
解得：k=12，
故选：B．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
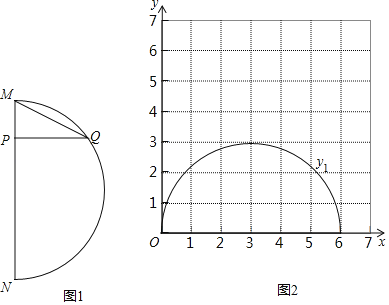
目标测试系列答案【题目】如图1，在弧MN和弦MN所组成的图形中，P是弦MN上一动点，过点P作弦MN的垂线，交弧MN于点Q，连接MQ．已知MN＝6cm，设M、P两点间的距离为xcm，P、Q两点间的距离为y1cm，M、Q两点间的距离为y2cm．小轩根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．下面是小轩的探究过程，请补充完整：
（1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：x/cm．
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 3.00 | 2.83 | 2.24 | 0 |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | m | 5.48 | 6 |
上表中m的值为 ．（保留两位小数）
（2）在同一平面直角坐标系xOy（图2）中，函数y1的图象如图，请你描出补全后的表中y2各组数值所对应的点（x，y2），并画出函数y2的图象；
（3）结合函数图象，解决问题：当△MPQ有一个角是30°时，MP的长度约为 cm．（保留两位小数）
【题目】根据学习函数的经验，探究函数y＝x2+ax﹣4|x+b|+4（b＜0）的图象和性质：
（1）下表给出了部分x，y的取值；
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知，a＝ ，b＝ ；
（2）用你喜欢的方式在坐标系中画出函数y＝x2+ax﹣4|x+b|+4的图象；
（3）结合你所画的函数图象，写出该函数的一条性质；
（4）若方程x2+ax﹣4|x+b|+4＝x+m至少有3个不同的实数解，请直接写出m的取值范围．
【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动．采取随机抽样的方式进行问卷调查．问卷调查的结果分为
、
、
、
四类．类表示非常了解；类表示比较了解；类表示基本了解；类表示不太了解．（要求每位同学必须选并且只能选择一项）统计数据整理如表：
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |
（1）表中
__________；
_________．
（2）根据表中数据，求出类同学数所对应的扇形圆心角为_________度．
（3）根据调查结果，请你估计该校1500名学生中对校训“非常了解”的人数；
（4）学校在开展了解校训意义活动中，需要从类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动，求恰好选中甲乙两人的概率？（请用列表法或是树状图表示）
