题目内容
【题目】如图，已知F是以AC为直径的半圆O上任意一点，过AC上任意一点H作AC的垂线分别交CF,AF的延长线于点E，B，点D是线段BE的中点.
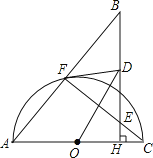
（1）求证：DF是⊙O的切线；
（2）若BF=AF，求证AF2=EF·CF.
【答案】（1）证明见解析;（2）证明见解析.
【解析】分析：（1）连接OF，根据圆周角定理得出∠AFC=90°，然后根据直角三角形斜边中线的性质求得DF=DE=
BE，根据等边对等角得出∠1=∠2，∠3=∠C，进而求得OF⊥DF，即可证得DF是 O的切线．（2）由∠C=∠BEF，∠EFB=∠AFC，可推出△EFB∽△AFC，进而推出
，即可求解.
本题解析：1)证明：如图1，连接OF，
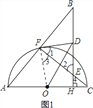
∵AC是直径∴∠AFC=90°∴∠BFE=90°，
∵D是BE的中点∴DF=DE=BE，∴∠1=∠2，
∵OF=OC，∴∠3=∠C，∴∠1+∠3=∠2+∠C=∠4+∠C，
∵BH⊥AC，∴在Rt△ECH中,∠4+∠C=90°，
∴∠1+∠3=90°，∴∠DFO=90°，∴OF⊥DF，
∴DF是O的切线。
（2）∵∠C=∠BEF，∠EFB=∠AFC, ∴△EFB∽△AFC，∴，即AF·BF= EF·CF,又BF=AF，∴AF2=EF·CF.
练习册系列答案
相关题目
