题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.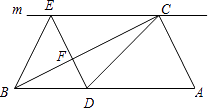
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)
【答案】
(1)
证明:∵直线m∥AB,
∴EC∥AD.
又∵∠ACB=90°,
∴BC⊥AC.
又∵DE⊥BC,
∴DE∥AC.
∵EC∥AD,DE∥AC,
∴四边形ADEC是平行四边形.
∴CE=AD
(2)
当点D是AB中点时,四边形BECD是菱形.
证明:∵D是AB中点,DE∥AC(已证),
∴F为BC中点,
∴BF=CF
∵直线m∥AB,
∴∠ECF=∠DBF.
∵∠BFD=∠CFE,
∴△BFD≌△CFE
∴DF=EF.
∵DE⊥BC,
∴BC和DE垂直且互相平分.
∴四边形BECD是菱形
(3)
当∠A的大小是45°时,四边形BECD是正方形.
理由是:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴四边形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形
【解析】(1)由BC⊥AC,DE⊥BC,得到DE∥AC,从而判断出四边形ADEC是平行四边形.即可,(2)先判断出△BFD≌△CFE,再判断出BC和DE垂直且互相平分,得到四边形BECD是菱形.(3)先判断出∠CDB=90°,从而得到有一个角是直角的菱形是正方形.
【考点精析】根据题目的已知条件,利用平行四边形的判定的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案