题目内容
【题目】阅读、操作与探究：
小亮发现一种方法，可以借助某些直角三角形画矩形，使矩形邻边比的最简形式（如4：6的最简形式为2：3）为两个连续自然数的比，具体操作如下：
如图1，Rt△ABC中，BC，AC，AB的长分别为3，4，5，先以点B为圆心，线段BA的长为半径画弧，交CB的延长线于点D，再过D，A两点分别作AC，CD的平行线，交于点E．得到矩形ACDE，则矩形ACDE的邻边比为 ．
请仿照小亮的方法解决下列问题：
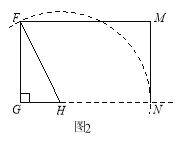
（1）如图2，已知Rt△FGH中，GH：GF：FH= 5：12：13，请你在图2中画一个矩形，使所画矩形邻边比的最简形式为两个连续自然数的比，并写出这个比值；
（2）若已知直角三角形的三边比为
（n为正整数），则所画矩形（邻边比的最简形式为两个连续自然数的比）的邻边比为 ．
【答案】1:2；(1)、2:3；(2)、n:(n+1).
【解析】
试题分析：(1)、根据题意中的画法得出矩形的邻边之比；(2)、根据题意画出图形得出比值；(3)、根据直角三角形的三边长进行化简，得出比值.
试题解析：1：2；
(1)、2：3；
(2)、
练习册系列答案
相关题目
