题目内容
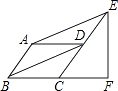
【题目】如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E. 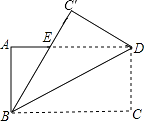
(1)判断△EBD的形状,并说明理由;
(2)求DE的长.
【答案】
(1)证明:∵△BDC1是由△BDC沿直线BD折叠得到的,
∴∠C1BD=∠CBD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CBD=∠EDB,
∴∠C1BD=∠EDB,
∴BE=DE,
∴△EBD是等腰三角形;
(2)解:设DE=x,则AE=AD﹣DE=8﹣x,
∵∠A=90°,BE=DE=x,
在Rt△ABE中,BE2=AB2+AE2,
∴x2=62+(8﹣x)2,
∴x= ![]() ,
,
即DE= ![]() .
.
【解析】(1)因为折叠前后∠DBC=∠DBC1,且平行,内错角相等,所以∠DCB=∠DAB,所以根据角之间的等量代换可得∠C1BD=∠EDB,根据等边对等角可知DE=BE;(2)设DE=x,则AE=AD﹣DE=8﹣x,在Rt△ABE中,根据勾股定理得:BE2=AB2+AE2,然后代入各值求解即可.
【考点精析】利用翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
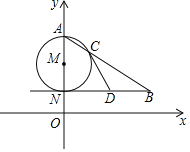
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)