题目内容
【题目】如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( ) 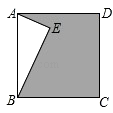
A.16
B.18
C.19
D.21
【答案】C
【解析】解:∵AE垂直于BE,且AE=3,BE=4,
∴在Rt△ABE中,AB2=AE2+BE2=25,
∴S阴影部分=S正方形ABCD﹣S△ABE
=AB2﹣ ![]() ×AE×BE
×AE×BE
=25﹣ ![]() ×3×4
×3×4
=19.
故选C.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目