Question

【题目】已知:在平面直角坐标系中,直线分别交、轴于点A、B两点,OA=5,∠OAB=60°.

(1)如图1,求直线AB的解析式；

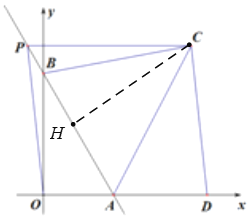
(2)如图2,点P为直线AB上一点，连接OP,点D在OA延长线上，分别过点P、D作OA、OP的平行线,两平行线交于点C，连接AC,设AD=m,△ABC的面积为S,求S与m的函数关系式;

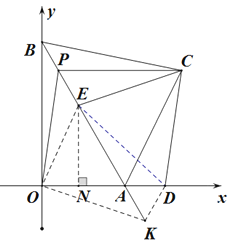
(3)如图3,在(2)的条件下,在PA上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE的周长等于22，求S的值.

Answer 1

【答案】(1)直线解析式为；(2)S=；(3).

【解析】

(1)先求出点B坐标，设AB解析式为，把点A(5，0)，B(0，)分别代入，利用待定系数法进行求解即可；

(2)由题意可得四边形ODCP是平行四边形，∠OAB=∠APC=60°，则有PC=OD=5+m，∠PCH=30°，过点C作CH⊥AB，在Rt△PCH中 利用勾股定理可求得CH=，再由S=ABCH代入相关数据进行整理即可得；

(3) 先求得∠PEC=∠ADC，设∠OPA=，则∠OPC= ∠ADC= ∠PEC=60°+，在BA延长线上截取AK=AD，连接OK，DK，DE，证明△ADK是等边三角形，继而证明△PEC≌△DKO，通过推导可得到OP=OK=CE=CD，再证明△CDE是等边三角形，可得CE=CD=DE，连接OE，证明△OPE≌△EDA，继而可得△OAE是等边三角形，得到OA=AE=5 ，根据四边形ADCE的周长等于22，可得ED=，过点E作EN⊥OD于点N，则DN=，由勾股定理得， 可得关于m的方程，解方程求得m的值后即可求得答案.

(1)在Rt△ABO中OA=5，∠OAB=60°，

∴∠OBA=30°，AB=10 ，

由勾股定理可得OB=，

∴B(0，)，

设AB解析式为，把点A(5，0)，B(0，)分别代入，得，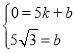

∴，

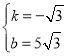∴直线解析式为；

(2)∵CP//OD，OP//CD，

∴四边形ODCP是平行四边形，∠OAB=∠APC=60°，

∴PC=OD=5+m，∠PCH=30°，

过点C作CH⊥AB，在Rt△PCH中 PH=，由勾股定理得CH=，

∴S=ABCH=；

(3) ∵∠ECD=∠OAB=60°，

∴∠EAD+∠ECD=180°，∠CEA+∠ADC=180°，

∴∠PEC=∠ADC，

设∠OPA=，则∠OPC= ∠ADC= ∠PEC=60°+，

在BA延长线上截取AK=AD，连接OK，DK，DE，

∵∠DAK=60°，

∴△ADK是等边三角形，

∴AD=DK=PE，∠ODK=∠APC，

∵PC=OD，

∴△PEC≌△DKO，

∴OK=CE，∠OKD=∠PEC=∠OPC=60°+， ∠AKD= ∠APC=60° ，

∴∠OPK= ∠OKB，

∴OP=OK=CE=CD，

又∵∠ECD=60°，

∴△CDE是等边三角形，

∴CE=CD=DE，

连接OE，∵ ∠ADE=∠APO，DE=CD=OP，

∴△OPE≌△EDA，

∴AE=OE， ∠OAE=60°，

∴△OAE是等边三角形，

∴OA=AE=5 ，

∵四边形ADCE的周长等于22，

∴AD+2DE=17，

∴ED=，

过点E作EN⊥OD于点N，则DN=，

由勾股定理得，

即，

解得，(舍去)，

∴S==20.