题目内容
【题目】如图，在直角坐标系中，已知直线y=-
x+4与y轴交于A点，与x轴交于B点，C点坐标为（﹣2，0）．
（1）求经过A，B，C三点的抛物线的解析式；
（2）如果M为抛物线的顶点，联结AM、BM，求四边形AOBM的面积．
【答案】（1）y=-
（2）31
【解析】分析：（1）先利用一次函数解析式确定A（0，4），B（8，0），再设交点式y=a（x+2）（x-8），然后把A点坐标代入求出a即可得到抛物线解析式；
（2）先利用配方法得到y=-
（x-3）2+
，则M（3，），作MD⊥x轴于D，如图，然后根据梯形面积公式和三角形面积公式，利用四边形AOBM的面积=S梯形AODM+S△BDM进行计算即可．
详解：
（1）当x=0时，y=-
x+4=4，则A（0，4），
当y=0时，- x+4=0，解得x=8，则B（8，0），
设抛物线解析式为y=a（x+2）（x﹣8），
把A（0，4）代入得a2（﹣8）=4，解得x=﹣ ，
∴抛物线解析式为y=﹣（x+2）（x﹣8），
即y=﹣x2+
x+4；
（2）∵y=﹣（x﹣3）2+，
∴M（3，），
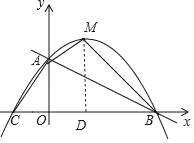
作MD⊥x轴于D，如图，
四边形AOBM的面积=S梯形AODM+S△BDM
=×（4+）×3+×5×
=31．
【题目】某智能手机越来越受到大众的喜爱，各种款式相继投放市场，某店经营的A款手机去年销售总额为50000元，今年每部销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
已知A，B两款手机的进货和销售价格如下表：
A款手机 | B款手机 | |
进货价格（元） | 1100 | 1400 |
销售价格（元） | 今年的销售价格 | 2000 |
（1）今年A款手机每部售价多少元？
（2）该店计划新进一批A款手机和B款手机共90部，且B款手机的进货数量不超过A款手机数量的两倍，应如何进货才能使这批手机获利最多？
