题目内容
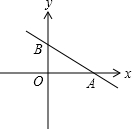 已知:如图,一次函数y=kx+b的图象与x轴、y轴分别交于点A(3,0),B(O,
已知:如图,一次函数y=kx+b的图象与x轴、y轴分别交于点A(3,0),B(O,| 3 |
| m |
| x |
(1)求一次函数的关系式;
(2)求m的值;
(3)O是原点,在线段OB的垂直平分线上是否存在一点P,使得△ABP的面积等于
| 1 |
| 2 |
分析:(1)由一次函数y=kx+b的图象与x轴、y轴分别交于点A(3,0),B(O,
),利用待定系数法即可求得此一次函数的关系式;
(2)由以AB为一边可以作两个等边△ABC,则顶点C有两个,分别为C1、C2,可设在第一象限的点C1(p,q),过C1作C1⊥AB于E,易证得C1A⊥x轴,则可求得C1的坐标;由∠ABO=60°,OB=
AB,易得C2(0,-
)也可使得△ABC是等边三角形,继而可求得m的值;
(3)由△ABP的面积等于
m,易得S△ABC=S△ABP;即可证得CP∥AB,即可求得直线CP的解析式,继而可求得P点的坐标.
| 3 |
(2)由以AB为一边可以作两个等边△ABC,则顶点C有两个,分别为C1、C2,可设在第一象限的点C1(p,q),过C1作C1⊥AB于E,易证得C1A⊥x轴,则可求得C1的坐标;由∠ABO=60°,OB=
| 1 |
| 2 |
| 3 |
(3)由△ABP的面积等于
| 1 |
| 2 |
解答:解:(1)∵一次函数y=kx+b的图象与x轴、y轴分别交于点A(3,0),B(O,
),
∴
,
解得:
,
故此一次函数的关系式为:y=-
x+
;
(2)以AB为一边可以作两个等边△ABC,则顶点C有两个,分别为C1、C2,
设在第一象限的点C1(p,q),过C1作C1⊥AB于E,
∵A(3,0),B(O,
),
∴OB=
,AB=
=2
,
∵△ABC1是等边三角形,
∴AC1=2
,AE=
,
∴AB=AC1,AE=OB,
∵在Rt△AOB和Rt△C1EA中,
,
∴Rt△AOB≌Rt△C1EA(HL),
∴∠BAO=∠AC1E=30°,
∴∠C1AO=90°,
∴C1A⊥x轴,
∴p=3,
过C1作C1F⊥y轴于F,
则四边形OAC1F是矩形,
∴OF=AC1=2
,
∴q=2
,
∴C1(3,2
);
∵C1点在y=
的图象上,
∴m=6
;
又∵OB=
,∠OBA=60°,
∴C2(0,-
),且C2点不可能在双曲线y=
的图象上,
∴m值只有一个,即m=6
;
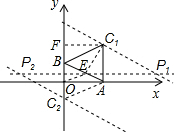 (3)存在.
(3)存在.
理由:∵P在OB的垂直平分线上,
∴P在第一象限或第二象限,
∴P点有两个,分别为P1,P2,
设在第一象限的点P1(a1,
),
根据题意,△ABP1的面积为:
m=3
,
∵S△ABC=
AB•CE=
×2
×3=3
,
∴S△ABC=S△ABP1,
设△ABP1中AB边上的高h,
由三角形的面积公式,当S△ABC=S△ABP1时,
则h=C1E,
∴C1P1∥AB,
设经过C1P1的直线的表达式为y1=k1x+b1,
则k1=k=-
,
∵C1(3,2
),代入y1=k1x+b1得:2
=-
×3+b1,
解得:b1=3
,
∴经过C1P1的直线的表达式为y1=-
x+3
,
点 P1(a1,
)在直线上C1P1上,
把点P1(a1,
)的坐标代入y1=-
x+3
,
∴
=-
×a1+3
,
∴a1=
;
同理,设在第二象限的点P2(a2,
),
设经过C2P2的直线的表达式为y2=k2x+b2,
∵点C2(0,-
)在直线y2=k2x+b2上,
∴k2=k=-
,b2=-
,
∴y2=-
x-
,
∵P2(a2,
)在直线y2=-
x-
上,
∴a2=-
,
∴P2(-
,
);
∴符合要求的P点有两个,分别为P1(
,
),P2(-
,
).
| 3 |
∴
|
解得:
|
故此一次函数的关系式为:y=-
| ||
| 3 |
| 3 |
(2)以AB为一边可以作两个等边△ABC,则顶点C有两个,分别为C1、C2,
设在第一象限的点C1(p,q),过C1作C1⊥AB于E,
∵A(3,0),B(O,
| 3 |
∴OB=
| 3 |
| OA2+OB2 |
| 3 |
∵△ABC1是等边三角形,
∴AC1=2
| 3 |
| 3 |
∴AB=AC1,AE=OB,
∵在Rt△AOB和Rt△C1EA中,
|
∴Rt△AOB≌Rt△C1EA(HL),
∴∠BAO=∠AC1E=30°,
∴∠C1AO=90°,
∴C1A⊥x轴,
∴p=3,
过C1作C1F⊥y轴于F,
则四边形OAC1F是矩形,
∴OF=AC1=2
| 3 |
∴q=2
| 3 |
∴C1(3,2
| 3 |
∵C1点在y=
| m |
| x |
∴m=6
| 3 |
又∵OB=
| 3 |
∴C2(0,-
| 3 |
| m |
| x |
∴m值只有一个,即m=6
| 3 |
 (3)存在.
(3)存在.理由:∵P在OB的垂直平分线上,
∴P在第一象限或第二象限,
∴P点有两个,分别为P1,P2,
设在第一象限的点P1(a1,
| ||
| 2 |
根据题意,△ABP1的面积为:
| 1 |
| 2 |
| 3 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S△ABC=S△ABP1,
设△ABP1中AB边上的高h,
由三角形的面积公式,当S△ABC=S△ABP1时,
则h=C1E,
∴C1P1∥AB,
设经过C1P1的直线的表达式为y1=k1x+b1,
则k1=k=-
| ||
| 3 |
∵C1(3,2
| 3 |
| 3 |
| ||
| 3 |
解得:b1=3
| 3 |
∴经过C1P1的直线的表达式为y1=-
| ||
| 3 |
| 3 |
点 P1(a1,
| ||
| 2 |
把点P1(a1,
| ||
| 2 |
| ||
| 3 |
| 3 |
∴
| ||
| 2 |
| ||
| 3 |
| 3 |
∴a1=
| 15 |
| 2 |
同理,设在第二象限的点P2(a2,
| ||
| 2 |
设经过C2P2的直线的表达式为y2=k2x+b2,
∵点C2(0,-
| 3 |
∴k2=k=-
| ||
| 3 |
| 3 |
∴y2=-
| ||
| 3 |
| 3 |
∵P2(a2,
| ||
| 2 |
| ||
| 3 |
| 3 |
∴a2=-
| 9 |
| 2 |
∴P2(-
| 9 |
| 2 |
| ||
| 2 |
∴符合要求的P点有两个,分别为P1(
| 15 |
| 2 |
| ||
| 2 |
| 9 |
| 2 |
| ||
| 2 |
点评:此题考查了待定系数法求函数的解析式、等边三角形的性质以及三角形面积问题.此题综合性强,难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 知
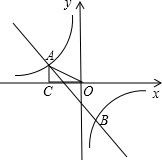
知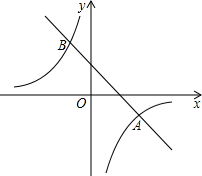 (2013•白云区一模)已知,如图,一次函数y=kx+b的图象与反比例函数y=
(2013•白云区一模)已知,如图,一次函数y=kx+b的图象与反比例函数y= 已知:如图,一次函数y=kx+b的图象与反比例函数
已知:如图,一次函数y=kx+b的图象与反比例函数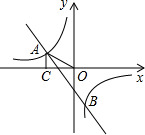 OA=
OA=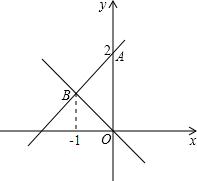 已知:如图,一次函数y=kx+b的图象与y轴交于点A,且与正比例函数y=-x的图象交于点B,则该一次函数的解析式为
已知:如图,一次函数y=kx+b的图象与y轴交于点A,且与正比例函数y=-x的图象交于点B,则该一次函数的解析式为