题目内容
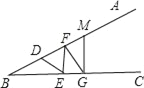
【题目】已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
【答案】(1)有4条,若∠ABC=10°,有8条;(2)n<![]() 的整数.
的整数.
【解析】
(1)根据已知可得到几组相等的角,再根据三角形外角的性质可得到∠EDF、∠FEG、∠AFG、∠AMG分别与∠B的关系,再根据三角形内角和定理即可求解.
(2)结合第(1)题,根据三角形内角和定理可知,需满足mn<90°,从而不难求解.
(1)有4条,若∠ABC=10°,有8条.
当∠ABC=20°,
∵BD=DE=EF=FG=GM,
∴∠DEB=∠B,∠EDF=∠EFD,∠FEG=∠FGE,∠GFM=∠FMG
∵∠EDF=2∠B=40°,∠FEG=3∠B=60°,∠AFG=4∠B=80°,∠AMG=5∠B=100°,
∴同理:∠AMG将成为下一个等腰三角形的底角
∵100°+100°>180°
∴不会再由下一条折线
∴共有四条拆线,分别是:DE、EF、FG,GM.
同理:当∠ABC=10°,有8条符合条件的折线.
(2)由(1)可知∠EDF=2∠B=2m°,∠FEG=3∠B=3m°,∠AFG=4∠B=4m°,
∵根据三角形内角和定理可知,需满足mn<90°,
∴n<![]() 的整数.
的整数.

练习册系列答案
相关题目