题目内容
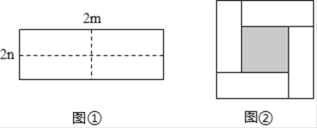
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:S小正方形= ;
方法二:S小正方形= ;
(2)(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系为
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x﹣y的值.
【答案】(1)(m+n)2﹣4mn,(m﹣n)2;;(2)(m+n)2﹣4mn=(m﹣n)2’(3) ±5.
【解析】
(1)观察图形可确定:方法一,大正方形的面积为(m+n)2,四个小长方形的面积和为4mn,中间阴影部分的面积为S=(m+n)2-4mn;
方法二,图2中阴影部分为正方形,其边长为m-n,所以其面积为(m-n)2.
(2)观察图形可确定,大正方形的面积减去四个小长方形的面积等于中间阴影部分的面积,即(m+n)2-4mn=(m-n)2.
(3)根据(2)的关系式代入计算即可求解.
(1)方法一:S小正方形=(m+n)2﹣4mn.
方法二:S小正方形=(m﹣n)2.
(2)由(1)可知,(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系为(m+n)2﹣4mn=(m﹣n)2.
(3)∵x+y=9,xy=14,
∴x﹣y=±![]() =±5.
=±5.
故答案为:(m+n)2﹣4mn,(m﹣n)2;(m+n)2﹣4mn=(m﹣n)2;±5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目