题目内容
 如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且点P(-1,-2)为双曲线上的一点,过P作PA垂直x轴于点A:
如图,已知正比例函数和反比例函数的图象都经过点M(-2,-1),且点P(-1,-2)为双曲线上的一点,过P作PA垂直x轴于点A:(1)写出正比例函数和反比例函数的关系式;
(2)若点Q为直线MO上一动点(不与点M、O重合),过点Q作QB⊥y轴于点B,是否存在点Q,使△OBQ与△OAP面积相等?如果存在,请求出点Q的坐标;如果不存在,请说明理由;
(3)在(2)的条件下,在平面内找一点C,使以O、P、C、Q为顶点的四边形为平行四边形,请直接写出C点坐标.
分析:(1)设反比例函数的解析式为y=
,正比例函数的解析式为y=k′x.把点M(-2,-1)分别代入其函数解析式,运用待定系数法即可求出对应的函数的关系式;
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,
x),使得△OBQ与△OAP面积相等,则B(0,
x).根据三角形的面积公式列出关于x的方程,解方程即可;
(3)利用在(2)的条件下,在平面内找一点C,使以O、P、C、Q为顶点的四边形为平行四边形,结合P,Q坐标以及平行四边形的对边相等,即可得出C点坐标.
| k |
| x |
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,
| 1 |
| 2 |
| 1 |
| 2 |
(3)利用在(2)的条件下,在平面内找一点C,使以O、P、C、Q为顶点的四边形为平行四边形,结合P,Q坐标以及平行四边形的对边相等,即可得出C点坐标.
解答:解:(1)设反比例函数的解析式为y=
(k≠0),正比例函数的解析式为y=k′x.
∵正比例函数和反比例函数的图象都经过点M(-2,-1),
∴-1=
,-1=-2k′,
∴k=2,k′=
.
∴正比例函数的解析式为y=
x,反比例函数的解析式为y=
.
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,
x),使得△OBQ与△OAP面积相等,则B(0,
x).
∵S△OBQ=S△OAP,
∴
•x×
x=
×2×1,
解得x=±2.
当x=2时,
x=1;
当x=-2时,
x=-1.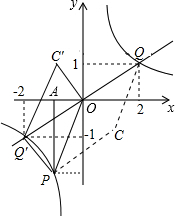
故在直线MO上存在这样的点Q(2,1)或(-2,-1),使得△OBQ与△OAP面积相等.
(3)如图所示:当四边形OPCQ是平行四边形,
∵P(-1,-2),Q(2,1),
∴C点坐标为;(1,-1),
当四边形OPQ′C′是平行四边形,
∵P(-1,-2),Q′(-2,-1),
∴C′点坐标为;(-1,1),
综上所述:使以O、P、C、Q为顶点的四边形为平行四边形,C点坐标为:(-1,1),(1,-1).
| k |
| x |
∵正比例函数和反比例函数的图象都经过点M(-2,-1),
∴-1=
| k |
| -2 |
∴k=2,k′=
| 1 |
| 2 |
∴正比例函数的解析式为y=
| 1 |
| 2 |
| 2 |
| x |
(2)当点Q在直线MO上运动时,假设在直线MO上存在这样的点Q(x,
| 1 |
| 2 |
| 1 |
| 2 |
∵S△OBQ=S△OAP,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得x=±2.
当x=2时,
| 1 |
| 2 |
当x=-2时,
| 1 |
| 2 |

故在直线MO上存在这样的点Q(2,1)或(-2,-1),使得△OBQ与△OAP面积相等.
(3)如图所示:当四边形OPCQ是平行四边形,
∵P(-1,-2),Q(2,1),
∴C点坐标为;(1,-1),
当四边形OPQ′C′是平行四边形,
∵P(-1,-2),Q′(-2,-1),
∴C′点坐标为;(-1,1),
综上所述:使以O、P、C、Q为顶点的四边形为平行四边形,C点坐标为:(-1,1),(1,-1).
点评:本题考查了运用待定系数法求函数的解析式及三角形的面积,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
相关题目
 边形OABD的面积S满足:S1=
边形OABD的面积S满足:S1= 如图,已知正比例函数y=ax与反比例函数y=
如图,已知正比例函数y=ax与反比例函数y= 标为1,过点A作x轴的垂线,垂足为M,连接BM.
标为1,过点A作x轴的垂线,垂足为M,连接BM. 如图,已知正比例函数y=kx的图象经过点A(-
如图,已知正比例函数y=kx的图象经过点A(- 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).