Question

【题目】如图，已知△ABC中，AB＝AC，点D、E分别在AB、AC上，且BD＝CE．

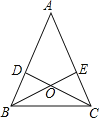
（1）找出图中所有的全等的三角形．

（2）选一组全等三角形进行证明．

Answer 1

【答案】（1）△ADC≌△AEB，△BCD≌△CBE，△BDO≌△CEO；（2）见解析.

【解析】

（1）根据题意可找出△ADC≌△AEB，△BCD≌△CBE，△BDO≌△CEO；

（2）根据等腰三角形的性质推出∠ABC=∠ACB，证△BCD≌△CBE．

（1）△ADC≌△AEB，△BCD≌△CBE，△BDO≌△CEO；

（2）∵AB＝AC，

∴∠ABC＝∠ACB（等边对等角），

在△BCD和△CBE中，

，

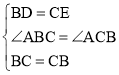∴△BCD≌△CBE，

∴∠CDB＝∠CEB，即∠ODB＝∠OEC，

∵BD＝CE，AB=AC

∴AD＝AE，

∵AD＝AE，∠A＝∠A，AC＝AB，

∴△ADC≌△AEB，

∵∠DOB＝∠EOC，∠ODB＝∠OEC，BD＝EC，

∴△BDO≌△CEO．