Question

【题目】在锐角中，，，，将绕点按逆时针方向旋转，得到．

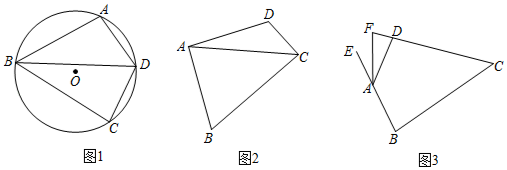
（1）如图1，当点在线段的延长线上时，求的度数；

（2）如图2，连接，．若的面积为4，求的面积；

（3）如图3，点为线段中点，点是线段上的动点，在绕点按逆时针方向旋转过程中，点的对应点是点，求线段长度的最小值．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）先根据旋转的性质得出，，再根据等腰三角形的性质可得，然后根据角的和差即可得；

（2）先根据旋转的性质得出，从而可得，再根据角的和差可得，然后根据相似三角形的判定定理得出，最后根据相似三角形的性质求解即可得；

（3）先根据旋转的性质确认点的运动轨迹，再根据点与圆的位置关系、垂线段最短确认最小时，点的位置，然后根据正弦三角函数值、线段的和差求解即可．

（1）由旋转的性质得，

∴

∴

故的度数为；

（2）由旋转的性质得

∴，，

∴，

∴

∴

∴

∵

∴

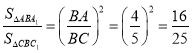
故的面积为；

（3）如图，在绕点按逆时针方向旋转过程中，点的运动轨迹在以点B为圆心，BP为半径的圆上

由点与圆的关系可知：当点在BA（或BA的延长线）与圆B的交点处，取得最小值，最小值为

因此，取得最小值时，长度也最小

由垂线段最短得：点P在AC上运动过程中，当时，BP取得最小值，最小值为

则所求的线段长度的最小值为．