题目内容
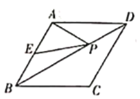
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
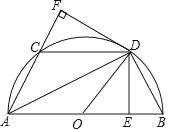
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
【答案】(1)证明见解析;(2)2![]() ;(3))2
;(3))2![]() .
.
【解析】
(1)根据角平分线的性质,可得DF与DE的关系,根据圆周角定理,可得DC与DB的关系,再根据HL,即可证明;(2)根据菱形的性质,可得OD与CD,OD与BD的关系,根据等边三角形的性质,可得∠DBA的度数,根据三角函数值,即可求解;(3)根据圆周角定理,可得OD⊥AB,根据勾股定理,即可求出AD的长.
(1)证明:∵![]() ,
,
∴CD=BD,∠FAD=∠BAD.
∵DF⊥AC,DE⊥AB,
∴DF=DE,∠BED=∠CFD=90°.
在Rt△CFD和Rt△BED中,![]()
∴△CDF≌△BDE(HL).
(2)四边形AODC是菱形时,
OD=CD=BD=OB,
∴∠DBA=60°,
∴AD=AB·sin∠DBA=4sin60°=2![]() .
.
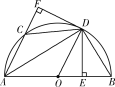
(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
由勾股定理得
AD=![]() =2
=2![]() .
.

【题目】为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机拍取40名学生进行问卷调查,其统计结果如表:
最喜欢的线上学习方式(没人最多选一种) | 人数 |
直播 | 10 |
录播 |
|
资源包 | 5 |
线上答疑 | 8 |
合计 | 40 |
(1)![]() ;
;
(2)若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播"对应扇形的圆心角度数;
(3)根据调查结果估计该校10000名学生中,最喜欢“线上答疑”的学生人数;
(4)在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.