题目内容
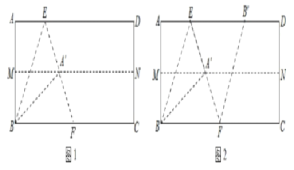
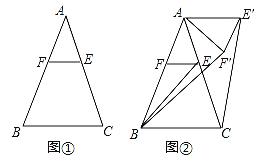
【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
【答案】(1)答案见解析;(2)①6;②36°或72°.
【解析】试题分析:(1)根据等腰三角形两底角相等∠B=∠C,再根据平行线的性质得出,∠AFE=∠A,∠AEF=∠C,得出∠AFE=∠AEF,进一步得出结论;
(2)求出AE=AF,再根据旋转的性质可得∠E′AC=∠F′AB,AE′=AF′,然后利用“边角边”证明△CAE′和△BAF′全等,根据全等三角形对应边相等证明即可;
(3)把△AEF绕点A逆时针旋转AE′与过点C与AB平行的直线相交于M、N,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
试题解析:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵EF∥BC,
∴∠AFE=∠A,∠AEF=∠C,
∴∠AFE=∠AEF,
∴AE=AF.
(2)①由旋转的性质得,∠E′AC=∠F′AB,AE′=AF′,
在△CAE′和△BAF′中,
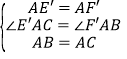 ,
,
∴△CAE′≌△BAF′(SAS),
∴CE′=BF′=6;
②由(1)可知AE=BC,
所以,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,如图,
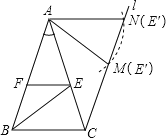
①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,
所以,∠BAM=∠ABC=72°,
又∵∠BAC=36°,
∴α=∠CAM=36°;
②当点E的像E′与点N重合时,
∵CE′∥AB,
∴∠AMN=∠BAM=72°,
∵AM=AN,
∴∠ANM=∠AMN=72°,
∴∠MAN=180°72°×2=36°,
∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,
综上所述,当旋转角α为36°或72°.