题目内容
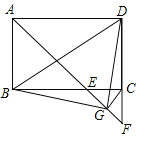
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.
与x轴交于A、B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴、y轴的交点.D为线段AB上一点.

(1)求抛物线的解析式及A点坐标.
(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.
(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′、B′D
①当点B′落坐标轴上时,求点D的坐标.
②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
【答案】(1)![]() ,A(﹣2,0);(2)E到BC的最大距离为
,A(﹣2,0);(2)E到BC的最大距离为![]() ;(3)①D1(0,0);D2(3
;(3)①D1(0,0);D2(3![]() ,0);②B′坐标为(0,3
,0);②B′坐标为(0,3![]() )或(-3
)或(-3![]() )或(
)或(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
(1)求出B,C两点的坐标,代入抛物线解析式即可得出答案;
(2)设E点横坐标为m,则F(m,m3),过点E作EH⊥BC于点H,EF=yFyE=![]() ,利用二次函数的性质可求出E到直线BC的距离的最大值;
,利用二次函数的性质可求出E到直线BC的距离的最大值;
(3)①点B′在以C为圆心,CB为半径的圆C上.所以满足条件的B′有两个,分别位于y轴、x轴,结合对称的性质解答即可;
②分不同的情况进行讨论:
(Ⅰ)当点B′位于y轴上,易得点B′的坐标;
(Ⅱ)如图3,连接CB′,构造菱形DB′CB,根据菱形的性质求得B′(3![]() ,3);
,3);
(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E、F,在直角△CFB′中,由勾股定理知m2+(5m)2=(3![]() )2,解出m即可;
)2,解出m即可;
(Ⅳ)如图5,∠AB′D=45°,连接CB’,过点B′作y轴的垂线,垂足为点F,由轴对称性质可得当∠AB′D=45°时,点A在线段CB′上,结合勾股定理求得m的值,进而求得符合条件的点B′的坐标.
(1)∵B点与C点是直线y=x﹣3与x轴、y轴的交点.
∴B(3,0),C(0,﹣3),
∴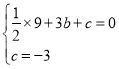 ,解得:
,解得: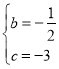 ,
,
∴抛物线的解析式为![]() ,
,
令y=0,则![]() ,
,
解得x1=﹣2,x2=3,
∴A(﹣2,0);
(2)设E点到直线BC的距离为d,E点横坐标为m,F(m,m﹣3),
∵B(3,0),C(0,﹣3),
∴∠OBC=45°,
如图1,过点E作EH⊥BC于点H,
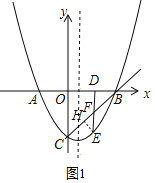
则△EFH为等腰直角三角形,
∴EH=![]() ,
,
EF=yF﹣yE=m﹣3﹣(![]() ),
),
=![]() (0≤m≤3),
(0≤m≤3),
=![]() ,
,
当![]() 时,EF的最大值为
时,EF的最大值为![]() ,
,
∴d=![]() EF=
EF=![]() =
=![]() .
.
即E到BC的最大距离为![]() ;
;
(3)①点B′在以C为圆心,CB为半径的圆C上;
(Ⅰ)当B′点落在x轴上时,D1(0,0);
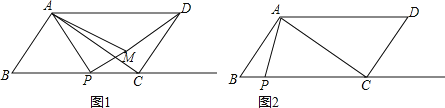
(Ⅱ)当B′点落在y轴上时,如图2,CB′=CB=3![]() ,
,

∵∠OB′D=45°
∴OD=OB’=3![]() ﹣3,
﹣3,
∴![]() ;
;
②分别画出图形进行讨论求解:
(Ⅰ)∠B′DA=45°时,如图2,OB′=3![]() ﹣3,B′(0,3
﹣3,B′(0,3![]() ﹣3)
﹣3)
(Ⅱ)如图3,连接CB′,∠B′DA=∠CBD=45°,

∴DB′∥BC,可得四边形DB′CB是菱形,
B′(﹣3![]() ,﹣3).
,﹣3).
(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E、F,
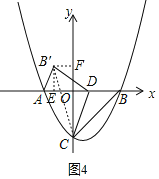
设线段FB’的长为m,B′E=AE=2﹣m,可得CF=5﹣m,
在直角三角形CFB’中,m2+(5﹣m)2=(3![]() )2,
)2,
解得m=![]() ,
,
故B′(![]() ),
),
(Ⅳ)如图5,∠AB′D=45°,连接CB’,过点B′作y轴的垂线,垂足为点F,

由轴对称性质可得,∠CB′D=∠CBD=45°,所以当∠AB′D=45°时,点A在线段CB′上,
∴![]() ,
,
设线段FB′的长为2m,FC=3m,(2m)2+(3m)2=![]() ,
,
解得:m=![]() ,B′
,B′ ,
,
综合以上可得B′坐标为(0,![]() )或
)或![]() 或(
或(![]() )或
)或 .
.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某厂设计了一款成本为20元∕件的公益用品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)认真分析上表中的数据,用你所学过的函数知识确定一个满足这些数据的y与x的函数关系,并求出函数关系式.
(2)设该厂试销该公益品每天获得的利润为w元,当销售单价x定为多少时,w有最大值?最大利润是多少?
(3)当地民政部门规定,若该厂销售此公益品单价不低于成本价且不超过46元/件时,该厂每销售一件此公益品,国家就补贴该厂a元利润(a>4)。设日销售利润为m元,公司通过销售记录发现,m始终随销售单价x的增大而增大,求a的取值范围.