题目内容
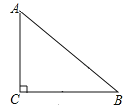
【题目】背景知识:如图,在![]() 中,
中,![]() ,若
,若![]() ,则:
,则:![]() .
.
(1)解决问题:
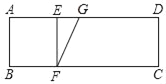
如图(1),![]() ,
,![]() ,
,![]() 是过点
是过点![]() 的直线,过点
的直线,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,现尝试探究线段
,现尝试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系:过点
之间的数量关系:过点![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,易发现图中出现了一对全等三角形,即
,易发现图中出现了一对全等三角形,即![]() ,由此可得线段
,由此可得线段![]() 、
、![]() 、
、![]() 之间的数量关系是: ;
之间的数量关系是: ;

(2)类比探究:
将图(1)中的![]() 绕点
绕点![]() 旋转到图(2)的位置,其它条件不变,试探究线段
旋转到图(2)的位置,其它条件不变,试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(3)拓展应用:
将图(1)中的![]() 绕点
绕点![]() 旋转到图 (3)的位置,其它条件不变,若
旋转到图 (3)的位置,其它条件不变,若![]() ,
,![]() ,则
,则![]() 的长为 (直接写结果).
的长为 (直接写结果).
【答案】(1)△EAC≌△BDC;BD+BA=![]() ;(2)BDBA=
;(2)BDBA=![]() ,证明见解析;(3)4.
,证明见解析;(3)4.
【解析】
(1)利用ASA证明出△EAC≌△BDC,从而得出AE=BD,EB=AE+AB=BD+AB,根据![]() 进一步得出答案即可;
进一步得出答案即可;
(2)过C作EC⊥CB交MN于E,利用ASA证明△ACE≌△DCB,进而求得线段之间的关系,进一步求证即可;
(3)过C作EC⊥CB于MN于E,利用ASA证明△ACE≌△DCB,然后进一步即可求出AB的长.
(1)∵![]() ,
,
∴∠ACE+∠ACB=90°,
∵![]() ,
,
∴∠BCD+∠ACB=90°
∴∠ACE=∠BCD,
在四边形ACDB中,
∵![]() ,
,![]() ,
,
∴∠CAB+∠D=180°,
∵∠CAB+∠EAC=180°
∴∠D=∠EAC,
在△EAC与△BDC中,
∵∠EAC=∠D,AC=DC,∠ACE=∠DCB,
∴△EAC≌△BDC(ASA),
∴AE=BD,EC=BC,
∴EB=AE+AB=BD+AB,
在Rt△ECB中,
∵EC=BC,
∴![]() ,
,
∴BD+BA=![]() ,
,
故答案为:△EAC≌△BDC;BD+AB=![]() ;
;
(2)BDBA=![]() ,
,
证明:
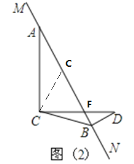
如图(2),过C作EC⊥CB交MN于E,则∠ECB=90°,
∴∠ECB+∠BCA=∠ACD+∠BCA,
∴∠ECA=∠BCD,
∵DB⊥MN,
∴∠ABD=∠ACD=90°,
记AC与BD的交点为F,则∠BFA=∠DFC,
∴∠BAF=∠FDC,
在△ACE与△DCB中,
∵∠BAF=∠FDC,AC=DC,∠ECA=∠BCD,
∴△ACE≌△DCB(ASA),
∴AE=BD,CE=CB,
∴在Rt△BCE中,BE=![]() ,
,
∴BD=AE=BA+BE=BA+![]() ,
,
即:BDBA=![]() ;
;
(3)
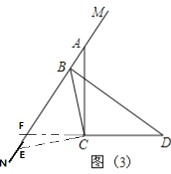
如图(3)过C作EC⊥CB于MN于E,MN与CD相交于F,
∵∠ACD=∠ACF=90°,∠ECB=90°,
∴∠ACB+∠BCF=∠BCF+∠ECF,
∴∠ACB=∠ECF,
∴∠ACB+90°=∠ECF+90°,
∴∠ACE=∠BCD,
∵DB⊥MN,
∴∠CAE=90°∠AFC,∠D=90°∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE与△DCB中,
∵∠ACE=∠BCD,AC=DC,∠CAE=∠D,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=![]() ,
,
又∵BE=ABAE=ABBD,
∴ABBD=![]() ,
,
∵BD=2,BC=![]() ,
,
∴AB=4.

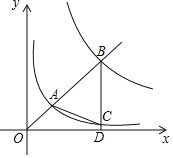
【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
250 | |
x |
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?