题目内容
在□ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并说明理由.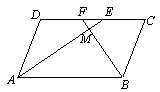
(1)证明见解析;(2)DF=CE.理由见解析.
解析试题分析:(1)因为AE,BF分别是∠DAB,∠ABC的角平分线,那么就有∠MAB=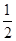 ∠DAB,∠MBA=
∠DAB,∠MBA=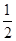 ∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.
∠ABC,而∠DAB与∠ABC是同旁内角互补,所以,能得到∠MAB+∠MBA=90°,即得证.
(2)两条线段相等.利用平行四边形的对边平行,以及角平分线的性质,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量减等量差相等,可证.
(1)∵在?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.(1分)
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
(2)线段DF与CE是相等关系,即DF=CE,
∵在?ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.(6分)
同理可得,CF=BC.
又∵在?ABCD中,AD=BC,
∴DE=CF.
∴DE-EF=CF-EF.
即DF=CE.
考点:1.相似三角形的判定与性质;2.角平分线的性质;3.平行四边形的性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目

 GE,试用含n的式子表示线段AN的长.
GE,试用含n的式子表示线段AN的长.

 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”; 的值;
的值;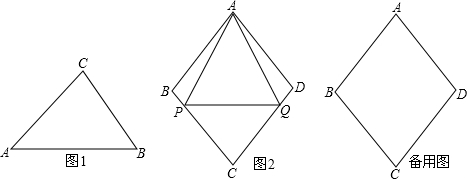





 S△EBH
S△EBH S△ABD
S△ABD S四边形ABCD
S四边形ABCD S四边形ABCD
S四边形ABCD