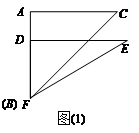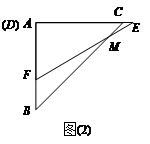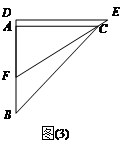题目内容
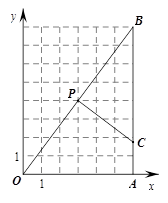
已知矩形OABC的顶点O(0,0)、A(4,0)、B(4,-3).动点P从O出发,以每秒1个单位的速度,沿射线OB方向运动.设运动时间为t秒.
(1)求P点的坐标(用含t的代数式表示);
(2)如图,以P为一顶点的正方形PQMN的边长为2,且边PQ⊥y轴.设正方形PQMN与矩形OABC的公共部分面积为S,当正方形PQMN与矩形OABC无公共部分时,运动停止.
①当t<4时,求S与t之间的函数关系式;
②当t>4时,设直线MQ、MN分别交矩形OABC的边BC、AB于D、E,问:是否存在这样的t,使得△PDE为直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
(1)(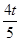 ,-
,-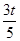 );(2)①当0<t≤
);(2)①当0<t≤ 时,S=
时,S=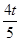 ×
×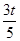 =
= t2 ;当
t2 ;当 <t≤
<t≤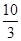 时,S=2×
时,S=2×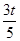 =
=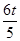 ;当
;当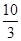 <t<4时,S=4;②t=5或
<t<4时,S=4;②t=5或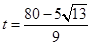 .
.
解析试题分析:(1)设PN与x轴交于点D,先由矩形的性质得出∠OAB=90°,在Rt△OAB中运用勾股定理求出OB=5,再由PD∥AB,得到△OPD∽△OBA,根据相似三角形对应边成比例得出OD=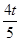 ,PD=
,PD=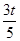 ,即可确定P点的坐标;
,即可确定P点的坐标;
(2)①分三种情况进行讨论:(i)当0<t≤ 时,设PQ与y轴交于点E,则S=S矩形ODPE=OD•PD;(ii)当
时,设PQ与y轴交于点E,则S=S矩形ODPE=OD•PD;(ii)当 <t≤
<t≤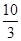 时,设PN与x轴交于点D,QM与x轴交于点F,则S=S矩形PQFD=PQ•PD;(iii)当
时,设PN与x轴交于点D,QM与x轴交于点F,则S=S矩形PQFD=PQ•PD;(iii)当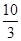 <t<4时,S=S正方形PQMN;
<t<4时,S=S正方形PQMN;
②分三种情况进行讨论:(i)当4<t≤5时,根据三角形外角的性质得出∠DPE>∠DBE=90°,则△PDE不可能为直角三角形;(ii)当t=5时,∠DPE=∠DBE=90°,此时,△PDE为直角三角形;(iii)当t>5时,由于∠DPE<∠DBE=90°,则当△PDE为直角三角形时,可能∠PDE=90°或者∠PED=90°.若∠PDE=90°,根据两角对应相等的两三角形相似得出△PQD∽△DME,得出PQ:DQ=DM:ME,列出关于t的方程,解方程即可;若∠PED=90°,则△PNE∽△EMD,根据两角对应相等的两三角形相似得出△PQD∽△DME,得出PQ:DQ=DM:ME,列出关于t的方程,解方程即可.
试题解析:(1)P(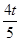 ,-
,-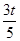 )
)
(2)①当0<t≤ 时,S=
时,S=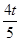 ×
×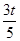 =
= t2
t2
当 <t≤
<t≤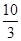 时,S=2×
时,S=2×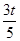 =
=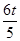
当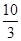 <t<4时,S=4
<t<4时,S=4
②当QM运动到AB位置时,恰好无公共部分,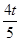 <4+2,即t<
<4+2,即t<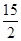 .
.
(ⅰ)当4<t<5时,∠DPE>∠DBE=90º,△PDE不可能为直角三角形
(ⅱ)当t=5时,∠DPE=∠DBE=90º,此时△PDE是直角三角形
(ⅲ)当5<t<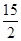 时,∠DPE<90º,还有两种可能,∠PDE=90º或∠PED=90º.
时,∠DPE<90º,还有两种可能,∠PDE=90º或∠PED=90º.
若∠PDE=90º,则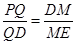 ,可得
,可得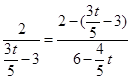 ,整理得9t2-160t+675=0,
,整理得9t2-160t+675=0,
解得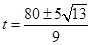 ,应取
,应取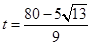
若∠PED=90º,则 ,可得
,可得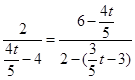 ,整理得8t2-115t+425=0,
,整理得8t2-115t+425=0,
注意到△<0,该方程无实数解(10分)
综上所述,符合条件的t的值有两个,t=5或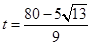 .
.
考点:相似形综合题.

 时,求AF及BE的长.
时,求AF及BE的长.
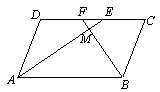

 ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
 ?
? ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.