Question

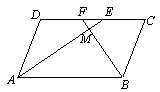
如图，在?ABCD中，E，F分别为BC，AB中点，连接FC，AE，且AE与FC交于点G，AE的延长线与DC的延长线交于点N．
（1）求证：△ABE≌△NCE；
（2）若AB=3n，FB=GE，试用含n的式子表示线段AN的长．

Answer 1

（1）证明见解析
（2）6n

解析试题分析：（1）根据平行四边形的性质可得AB∥CN，由此可知∠B=∠ECN，再根据全等三角形的判定方法ASA即可证明△ABE≌△NCE；
（2）因为AB∥CN，所以△AFG∽△CNG，利用相似三角形的性质和已知条件即可得到含n的式子表示线段AN的长．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AB∥CN，
∴∠B=∠ECN，
∵E是BC中点，
∴BE=CE，
又∵∠AEB=∠CEN，
∴△ABE≌△NCE
（2）∵△ABE≌△NCE，
∴AB=CN，AE=NE
∵AB∥CN，
∴△AFG∽△CNG，AF=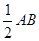
∴AF：CN=AG：GN=1：2，
∵AE+NE=AG+GN，
∴AG=2GE，EN=3GE
∵AB=3n，FB=GE=，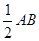
∴GE=n,AG=2n,EN=3n
∴AN=AG+GE+EN=6n．
考点：1、平行四边形的性质；2、全等三角形的判定与性质；3、相似三角形的判定与性质