题目内容
(1)解方程:x2+2x-1=0.
(2)解不等式组:
,并将解集在数轴上表示出来.
(2)解不等式组:
|
(1)由原方程移项,得
x2+2x=1,
等式两边同时加上一次项系数2的一半的平方,得
x2+2x+1=2,
配方,得
(x+1)2=2,
解得,x=-1±
,
即x1=-1+
,x2=-1-
;
(2)
不等式①的解集是:x≤4;
不等式②的解集是:x>
;
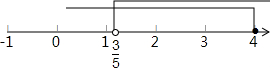
故该不等式组的解集是:
<x≤4,表示在数轴上为:
x2+2x=1,
等式两边同时加上一次项系数2的一半的平方,得
x2+2x+1=2,
配方,得
(x+1)2=2,
解得,x=-1±
| 2 |
即x1=-1+
| 2 |
| 2 |
(2)
|
不等式①的解集是:x≤4;
不等式②的解集是:x>
| 3 |
| 5 |
故该不等式组的解集是:
| 3 |
| 5 |


练习册系列答案
相关题目