题目内容
【题目】矩形![]() 中,
中,![]() 为
为![]() 中点、
中点、![]() 为
为![]() 中点,
中点,![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() 并延长交
并延长交![]() 与点
与点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.

【答案】证明见解析.
【解析】
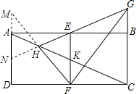
设AC、EF相交于点K,延长FH与DA的延长线相交于点M,延长GH与AD相交于点N,求出△AMH和△KFH相似,根据相似三角形对应边成比例可得![]() =
=![]() ,求出△ANH和△KEH相似,根据相似三角形对应边成比例可得
,求出△ANH和△KEH相似,根据相似三角形对应边成比例可得![]() =
=![]() ,然后求出AM=AN,再利用“角边角”证明△AEN和△BEG全等,根据全等三角形对应边相等可得AN=BG,然后求出DM=CG,再利用“边角边”证明△DFM和△CFG全等,根据全等三角形对应角相等可得∠M=∠CGF,然后根据平行线的性质可得∠HFE=∠M,∠EFG=∠CGF,再等量代换即可得证.
,然后求出AM=AN,再利用“角边角”证明△AEN和△BEG全等,根据全等三角形对应边相等可得AN=BG,然后求出DM=CG,再利用“边角边”证明△DFM和△CFG全等,根据全等三角形对应角相等可得∠M=∠CGF,然后根据平行线的性质可得∠HFE=∠M,∠EFG=∠CGF,再等量代换即可得证.
证明:如图,设![]() 、
、![]() 相交于点
相交于点![]() ,延长
,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,延长
,延长![]() 与
与![]() 相交于点
相交于点![]() ,
,
∵![]() 为
为![]() 中点、
中点、![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点、
中点、![]() 为
为![]() 中点,
中点,![]() 是对角线,
是对角线,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
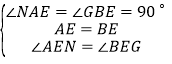 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
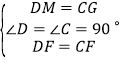 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目