题目内容
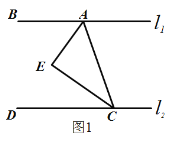
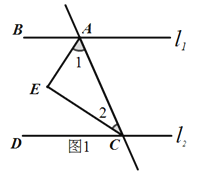
【题目】如图1,点A、B在直线![]() 上,点C、D在直线
上,点C、D在直线![]() 上,AE平分∠BAC,CE平分∠ACD,
上,AE平分∠BAC,CE平分∠ACD,
∠EAC+∠ACE=90° .
(1)请判断![]() 与
与![]() 的位置关系并说明理由;
的位置关系并说明理由;
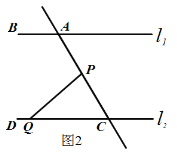
(2)如图2,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(不与点C重合)∠CPQ+∠CQP与∠BAC有何数量关系?请说明理由.
【答案】(1)![]() ∥
∥![]() ;(2)①当Q在C点左侧时,∠BAC=∠CQP +∠CPQ,②当Q在C点右侧时,∠CPQ+∠CQP+∠BAC=180°.
;(2)①当Q在C点左侧时,∠BAC=∠CQP +∠CPQ,②当Q在C点右侧时,∠CPQ+∠CQP+∠BAC=180°.
【解析】(1)先根据CE平分∠ACD,AE平分∠BAC得出∠BAC=2∠1,∠ACD=2∠2,再由∠1+∠2=90°可知∠BAC+∠ACD=180,故可得出结论;
(2)分两种情况讨论:①当Q在C点左侧时;②当Q在C点右侧时.
(1)![]() ∥
∥![]() .理由如下:
.理由如下:
∵AE平分∠BAC,CE平分∠ACD(已知),
∴∠BAC=2∠1,∠ACD=2∠2(角平分线的定义);
又∵∠1+∠2=90°(已知),
∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°(等量代换)
∴![]() ∥
∥![]() (同旁内角互补,两直线平行)
(同旁内角互补,两直线平行)
(2)①当Q在C点左侧时,过点P作PE∥![]() .
.
∵![]() ∥
∥![]() (已证),
(已证),
∴PE∥![]() (同平行于一条直线的两直线互相平行),
(同平行于一条直线的两直线互相平行),
∴∠1=∠2,(两直线平行,内错角相等),
∠BAC=∠EPC,(两直线平行,同位角相等),
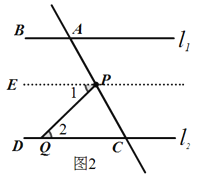
又∵∠EPC=∠1+∠CPQ,
∴∠BAC=∠CQP +∠CPQ(等量代换)
②当Q在C点右侧时,过点P作PE∥![]() .
.
∵![]() ∥
∥![]() (已证),
(已证),
∴PE∥![]() (同平行于一条直线的两直线互相平行),
(同平行于一条直线的两直线互相平行),
∴∠1=∠2,∠BAC=∠APE,(两直线平行,内错角相等),
又∵∠EPC=∠1+
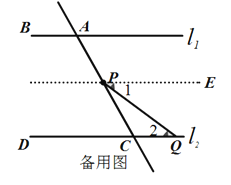
∠APE+∠EPC=180°(平角定义)
∴∠CPQ+∠CQP+∠BAC=180°.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案