题目内容
【题目】如图，四边形
中，已知
，
，对角线
平分
，
，
，则边
的长度为________．
【答案】
或
【解析】
如图，作辅助线；首先证明△FBD∽△GDA，进而得到DGDF=BFAG①；设BE=λ，将①式中的线段分别用λ来表示，得到关于λ的方程，解方程即可解决问题．
解：如图，
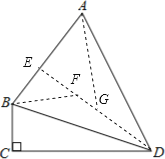
过点D作DE⊥AB于点E；在ED上截取EF=EB，EG=EA；
连接AG，BF；则∠BFE=∠AGE=45°，
∴∠BFD=∠DGA=135°；
∵BD平分∠ABC，且∠BCD=90°，
∴DE=DC=12，BE=BC；
∵∠FBD+∠BDF=∠BDF+∠ADG=45°，
∴∠FBD=∠GDA；
∴△FBD∽△GDA，
∴
＝
，即DGDF=BFAG；
设BE=λ，则DF=12-λ，EG=EA=10-λ；
BF=
λ，AG=EG=（10-λ），
∴（λ+2）（12-λ）=（10-λ）λ，
整理得：λ2-10λ+24=0，
解得：λ=4或6，
即边BC的长度为4或6．
由勾股定理得：BD2=BC2+CD2，
∴BD=4
或6
故答案为：4或6．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
【题目】己知二次函数
中，函数
与自变量
的部分对应值如下表:
| … |
| 0 | 1 | 2 | 3 | 4 | … |
| … | 10 | 5 | 2 | 1 | 2 | 5 | … |
（1）求该二次函数的解析式;
（2）当为何值时，有最小值，最小值是多少?
（3）若
，
两点都在该函数的图像上，试比较
与
的大小.
