题目内容
【题目】如图,一次函数![]() 的图像交x轴、y轴于A、B两点
的图像交x轴、y轴于A、B两点
(1)直接写出A、B两点的坐标:____________;______________。
(2)P为线段AB上一点,PQ//y轴交x轴于C,交双曲线![]() 于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
于Q且四边形OBPQ为平行四边形,△OCQ的面积为3
① 求k的值和P点坐标;
② 将△OBP绕点O逆时针旋转一周,在整个旋转过程中,P点能否落在双曲线![]() 上?请说明理由.
上?请说明理由.

【答案】 (4,0) (0,-2)
【解析】分析:(1)利用图象与坐标轴交点坐标求法分别求出A,B两点坐标即可;
(2)①根据![]() 的面积为3,得出
的面积为3,得出![]() ,即可得出
,即可得出![]() ,再利用
,再利用![]() 得出QC与OC的长,即可得出P点坐标;
得出QC与OC的长,即可得出P点坐标;
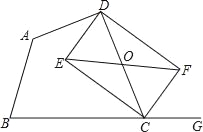
②作第一象限角的角平分线OD,交反比例函数![]() 的图象于点D,首先得出OE2=6,以及OD2=12,进而得出OP>OD,即可得出答案.
的图象于点D,首先得出OE2=6,以及OD2=12,进而得出OP>OD,即可得出答案.
详解:(1)∵一次函数![]() 的图象分别交x轴、y轴于A.B两点,
的图象分别交x轴、y轴于A.B两点,
∴当图象与x轴相交,y=0时,0=![]() ,解得:x=4,
,解得:x=4,
当图象与y轴相交,x=0时,y=2,
故A(4,0),B(0,2);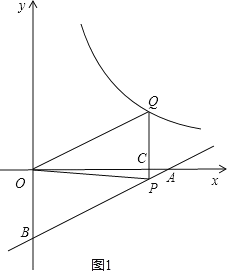
(2)①∵△OQC的面积为3,∴OC×CQ=6,∴k=6,
在平行四边形OBPQ中,OB//QP,OB=QP,OQ//AB,
∴∠QCO=∠BOA,∠QOC=∠BAO,
∴△QCO∽△BOA,
∴![]() ,∴OC=2QC,
,∴OC=2QC,
∵OC×CQ=6,
∴![]()
∴点P的坐标为![]()
②在Rt△OCP中,![]()
作第一象限角的角平分线OD,交反比例函数![]() 的图象于点D,
的图象于点D,
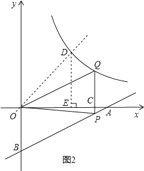
则OD的长是点O到反比例函数![]() 的图象上各点的最短距离,
的图象上各点的最短距离,
过点D作DE⊥OA于点E,
则![]()
∴![]()
∴OP>OD,
∴旋转后点P′能在反比例函数![]() 的图象上.
的图象上.

练习册系列答案
相关题目