题目内容
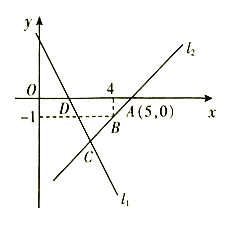
【题目】如图,直线![]() 的函数解析式为
的函数解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点
交于点![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍?如果存在,请求出
倍?如果存在,请求出![]() 坐标;如果不存在,请说明理由.
坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)3;(3)在直线
;(2)3;(3)在直线![]() 上存在点
上存在点![]() 或
或![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍.
倍.
【解析】
(1)根据点A、B的坐标利用待定系数法即可求出直线l2的函数解析式;
(2)令y=-2x+4=0求出x值,即可得出点D的坐标,联立两直线解析式成方程组,解方程组即可得出点C的坐标,再根据三角形的面积即可得出结论;
(3)假设存在点P,使得△ADP面积是△ADC面积的1.5倍,根据两三角形面积间的关系|yP|=1.5|yC|=3,再根据一次函数图象上点的坐标特征即可求出点P的坐标.
解:(1)设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的函数解析式为
的函数解析式为![]() .
.
(2)联立两直线解析式成方程组,
![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
(3)假设存在.
![]() 面积是
面积是![]() 面积的
面积的![]() 倍,
倍,
![]() ,
,
当![]() 时,
时,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
综上所述:在直线![]() 上存在点
上存在点![]() 或
或![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍.
倍.
故答案为:(1)![]() ;(2)3;(3)在直线
;(2)3;(3)在直线![]() 上存在点
上存在点![]() 或
或![]() ,使得
,使得![]() 面积是
面积是![]() 面积的
面积的![]() 倍.
倍.

 阅读快车系列答案
阅读快车系列答案【题目】![]() 年
年![]() 月
月![]() 日是第
日是第![]() 个世界读书日,为迎接第
个世界读书日,为迎接第![]() 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按![]() 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.