题目内容
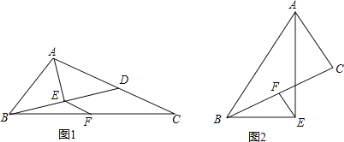
【题目】如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据线段垂直平分线的性质,可得AF=CF,再根据等角的余角相等可得∠B=∠BAF,所以AF=BF.
(2)由AAS可证△AEG≌△CEF,所以AG=CF.由一组对边平行且相等的四边形是平行四边形得四边形AFCG是平行四边形,进而证得四边形AFCG是菱形,最后根据有一个角为直角的菱形是正方形得证四边形AFCG是正方形.
证明 (1)∵AD=CD,点E是边AC的中点,
∴DE⊥AC.
即得DE是线段AC的垂直平分线.
∴AF=CF.
∴∠FAC=∠ACB.
在Rt△ABC中,由∠BAC=90°,
得∠B+∠ACB=90°,∠FAC+∠BAF=90°.
∴∠B=∠BAF.
∴AF=BF.
(2)∵AG∥CF,
∴∠AGE=∠CFE.
又∵点E是边AC的中点,
∴AE=CE.
在△AEG和△CEF中,
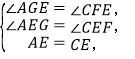
∴△AEG≌△CEF(AAS).
∴AG=CF.
又∵AG∥CF,
∴四边形AFCG是平行四边形.
∵AF=CF,
∴四边形AFCG是菱形.
在Rt△ABC中,由AF=CF,AF=BF,得BF=CF.
即得点F是边BC的中点.
又∵AB=AC,
∴AF⊥BC.即得∠AFC=90°.
∴四边形AFCG是正方形.

【题目】将正整数![]() 至
至![]() 按照一定规律排成下表:
按照一定规律排成下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…… |
记![]() 表示第
表示第![]() 行第
行第![]() 个数,如
个数,如![]() 表示第
表示第![]() 行第
行第![]() 个数是
个数是![]() .
.
(1)直接写出![]() _______________,
_______________,![]() _______________;
_______________;
(2)①如果![]() ,那么
,那么![]() _________________,
_________________,![]() ________;②用
________;②用![]() ,
,![]() 表示
表示![]() __________;
__________;
(3)将表格中的![]() 个阴影格子看成一个整体并平移,所覆盖的
个阴影格子看成一个整体并平移,所覆盖的![]() 个数之和能否等于
个数之和能否等于![]() .若能,求出这
.若能,求出这![]() 个数中的最小数,若不能说明理由.
个数中的最小数,若不能说明理由.