题目内容
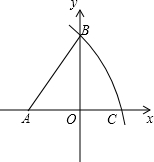
如图,在平面直角坐标系中,点A,B的坐标分别为(-6,0)、(0,8).以点A为圆心,以AB长为半径画弧,交x正半轴于点C,则点C的坐标为( ).

(4,0)
首先利用勾股定理求出AB的长,进而得到AC的长,因为OC=AC-AO,所以OC求出,继而求出点C的坐标.
解:∵点A,B的坐标分别为(-6,0)、(0,8),
∴AO=6,BO=8,
∴AB=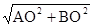 =10,
=10,
∵以点A为圆心,以AB长为半径画弧,
∴AB=AC=10,
∴OC=AC-AO=4,
∵交x正半轴于点C,
∴点C的坐标为(4,0),
故答案为:(4,0).
解:∵点A,B的坐标分别为(-6,0)、(0,8),
∴AO=6,BO=8,
∴AB=
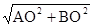 =10,
=10,∵以点A为圆心,以AB长为半径画弧,
∴AB=AC=10,
∴OC=AC-AO=4,
∵交x正半轴于点C,
∴点C的坐标为(4,0),
故答案为:(4,0).

练习册系列答案
相关题目
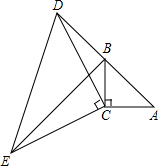
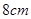 的正方形
的正方形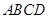 折叠,使点
折叠,使点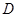 落在
落在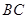 边中点
边中点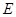 处,点
处,点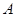 落在点
落在点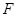 处,折痕为
处,折痕为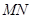 ,则
,则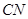 的长为 .
的长为 .